PVSOL Premium 2020补丁

　　PVSOL Premium补丁是一款针对刚发布的PVSOL Premium 2020而开发，可以将官方版直接激活，从而解除所有功能限制，让用户能够永久免费使用此工具进行设计；新版本PVSOL的所有其它设计类型都会提供给用户，而设计人员只需要选择最适合您的光伏项目的设计类型，详细结果始终提供有关系统性能的信息；使用PVSOL，无论是计算自耗，设计电池存储或集成电动汽车，您都可以立即实现并提出所有客户的愿望，可以随时使用我们广泛的产品数据库；用户可以为客户生成高质量的项目报告，可以根据需要进行配置和编辑，也可以创建带有必要安全装置的电路图；喜欢的用户可以下载体验

软件功能

　　优化模块互连

　　您可以决定是要将多个模块区域连接到一个逆变器，还是要为每个模块区域选择一个单独的逆变器，或者将两者组合。

　　系统的当前状态检查是否已完成互连，互连窗口中随时会显示单个逆变器和MPP跟踪器。

　　当前的在线数据库

　　在我们广泛的产品数据库中，您目前可以找到超过19,500个光伏模块，4,700个逆变器，1,400个电池系统以及许多其他产品的数据记录

　　例如电动车和性能优化器，这些记录已由各自的制造商进行了更新。

　　借助我们的在线数据库，您可以轻松地将自己的产品提供给他人。

　　详细的项目报告

　　创建具有20种语言的模拟结果和技术详细信息的综合项目报告，并将其导出为Word或PDF文档。

　　为了使外观专业，可以将公司徽标添加到标题页并指定应在报告中显示的内容。

　　带电池存储的

　　并网系统通过选择使用的电池并定义电池逆变器和充电策略来设计自己的电池存储系统。

　　或者，您可以为领先制造商的电池系统充电。

　　电动汽车

　　选择一种或多种与光伏系统结合模拟的电动汽车。

　　通过输入每日里程和停机时间，PV SOL计算出可用于为电动汽车充电的PV能量。

　　结果摘要

　　详细的结果概述包含模拟结果的表示形式，成本效益的结果以及详细的表格化能量平衡以及所发生的所有收益和损失。

　　地毯图将立即为您提供单个结果的年度概览。

软件特色

　　电路图

　　PVSOL通过可自由配置的电路图支持您的系统设计。

　　可以确定每个逆变器的电缆串损耗以及交流和直流电缆损耗。

　　可以轻松添加许多安全装置，例如保险丝，隔离开关和电涌保护器。

　　其他功能

　　选择要用于散射辐射和倾斜表面上辐射的模型。

　　需要时可以生成每个时间步长的UI和UP特性。

　　交换您的用户ID，以在公司内共享自己创建的产品。

　　PVSOL需要处理器时间，RAM和硬盘空间等资源来存储临时文件。

　　根据项目的规模，这些要求会有所不同，并且难以量化，需要互联网连接。

安装步骤

　　1、用户可以点击本网站提供的下载路径下载得到对应的程序安装包

　　2、只需要使用解压功能将压缩包打开，双击主程序即可进行安装，弹出程序安装界面

　　3、同意上述协议条款，然后继续安装应用程序，点击同意按钮即可

　　4、可以根据自己的需要点击浏览按钮将应用程序的安装路径进行更改

　　5、现在准备安装主程序，点击安装按钮开始安装

　　6、弹出应用程序安装进度条加载界面，只需要等待加载完成即可

　　弹出以下界面，用户可以直接使用鼠标点击下一步按钮，根据提示安装一个组件，然后会继续安装

　　7、根据提示点击安装，弹出程序安装完成界面，点击完成按钮即可

方法

　　1、程序安装完成后，先不要运行程序，打开安装包，然后将文件夹内的文件复制到粘贴板

　　2、然后打开程序安装路径，把复制的文件粘贴到对应的程序文件夹中替换源文件

　　3、完成以上操作步骤后，就可以双击应用程序将其打开，此时您就可以得到对应程序

使用说明

　　光伏组件

　　可以根据PV发电机倾斜表面上的辐射和计算出的模块温度来确定PV模块的功率输出。对于每种辐照和温度，可以在任何数量的操作点上操作PV模块。这些工作点描述了模块的电气特性。

　　工作点和特点

　　图1显示了标称功率为280 W的模块在不同辐照值和模块温度为25°C时的特性。原则上，该模块可以在所示的特性曲线上的任何一点上运行。功率输出基于电压和产生的电流的乘积。

　　示例：模块以1000 W /m²辐射，模块温度为25°C。这导致了图1中的上部特性曲线。如果模块以44 V工作，则它提供0 A的电流，模块功率为44 V·0 A = 0W。因此，模块处于空闲状态。如果模块在0 V的电压下运行（即发生短路），则确实可以提供超过8 A的电流，但是由于0 V 8.2 A = 0 W，模块也不产生任何功率。

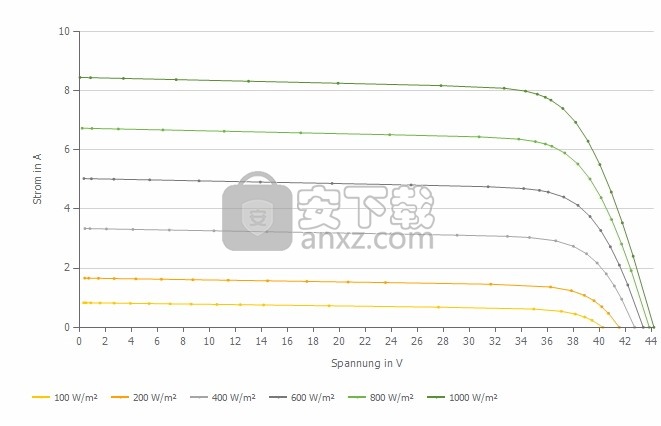
　　图1：具有不同辐射水平的280 W模块的特性曲线。

　　但是，对于特性在0 V（短路）和44 V（空载）之间的其他每个点，都有大于0 W的功率。如果将这些功率中的每一个相对于选定的电压作图，就会获得图2的特性曲线。

　　在此清楚的是，模块的功率输出最初随着模块的电压增加而增加。在约36 V时，功率达到约280 W的峰值，此后功率又下降。在44 V时，功率再次变为0。

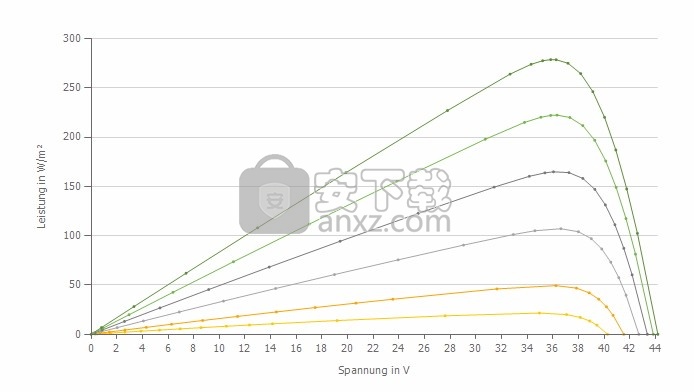
　　图2：具有不同辐射水平的280 W模块的性能曲线。

　　模块提供最大功率的点称为MPP（最大功率点，德语：最大功率点）。

　　因此，对于光伏系统的运行，重要的是尽可能在MPP中的最大功率点运行模块，以便从系统中获得最大的产量。此时，查找此MPP并操作模块的任务由安装在逆变器中的MPP跟踪器执行。

　　1.2。模块温度

　　组件温度对PV组件的特性曲线有很大影响。

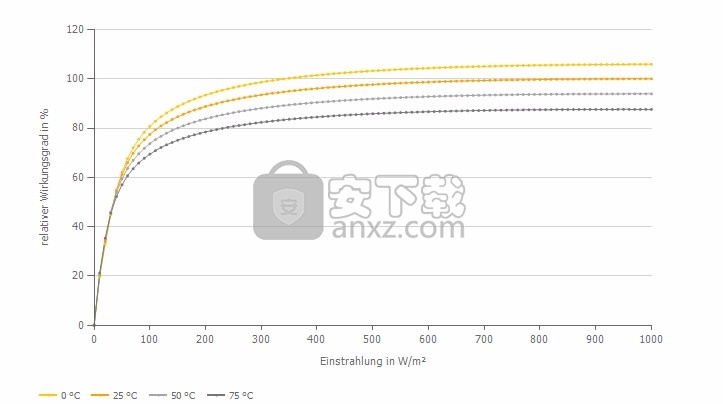
　　图3：不同模块温度下模块效率的典型过程。

　　模块会根据安装情况，模块容量，模块安装类型和辐射而发热。

　　以一小时的仿真间隔，根据辐射E和温度偏移来静态计算模块温度，具体取决于安装类型：

　　Tmodul = Tamb + DT * E / ESTC

　　表1：温度DT与外界温度相比的增加例如为。辐射ESTC = 1000 W /m²

　　DT安装情况

　　平行于屋顶的29 K，通风良好

　　32 K屋顶集成-后通风

　　集成于屋顶的43 K-不背面通风

　　高架28 K-屋顶

　　高架22 K-开放空间

　　资料来源：DGS光伏系统指南，第三版

　　由于静态温度模型没有考虑模块的热惯性，因此它不适合在几分钟内使用可变辐射进行仿真。因此，动态温度模型用于一分钟的仿真间隔。该模块用电容C表示，模块温度为Tmodule：

　　dQ / dt = C * dTmodule / dt

　　为了计算热容量C，根据模块数据集使用了830 J / kg / K的比热容量和模块质量。

　　模块被辐射加热。这可以通过热量损失来抵消：

　　dQlosses / dt = UA *（Tmodul-Tamb）

　　热量损失率UA由静态温度偏移确定：UA =确定的ESTC / DT。

　　2.特征模型

　　为了描述太阳能电池的特性，使用了一个模型，该模型的任务是在尽可能广泛的外部影响范围内表示电池的电或热行为。

　　基本上，模型可以分为经验模型和物理模型。经验模型基于真实光伏模块或电池的测量结果，通常会从中获得拟合函数的参数。这些模型可以为测得的模块实现非常高的映射精度，而正如预期的那样，它们在未测得的模块中效果较差，因为此处未调整任何参数。

　　物理模型试图以通常有效的方式表示光伏半导体中的实际过程。这意味着它们也可以以一定的精度在仅由制造商进行最少测量的模块上使用。但是，也设置物理模型之前带有一些参数，这些参数也必须凭经验确定，或者以标准值的形式并入建模中。最广泛使用的物理模型是一个和两个二极管模型。

　　2.1。 PV *SOL®模型

　　2.1.1。基本

　　它主要是一个数学模型，但是除了制造商提供的作为无条件输入变量的电气数据之外，它还需要在接近STC辐射20％的部分负载点处提供另一组电气数据。它根据辐射利用填充因子的特性曲线。由于短路电流从辐照很大程度上是线性的，因此可以使用填充因子函数从中得出MPP中的值。一旦计算出这些数量，就将对这三个点进行指数插值。 PV *SOL®模型可以针对给定的辐射直接计算模块的关键参数和特性曲线。

　　2.1.2。部分负荷点

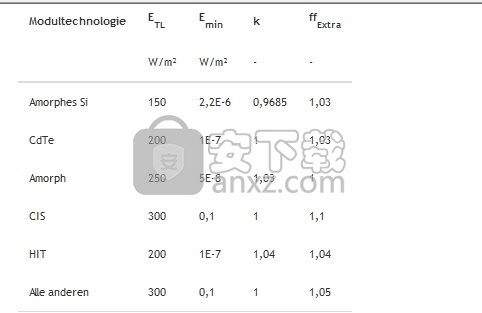
　　如果无法获得有关部分负荷点所需的附加信息-理想情况下由模块制造商提供-根据模块技术计算标准值。

　　为此，首先确定一些参数。在部分负载点ETL处的辐照确定填充系数在何处呈现（最大值）值ffExtra·FFSTC。参数Emin和k用于迭代确定其他参数。

　　首先计算部分负荷填充系数：

　　（2-1-1）

　　部分负载点的空载电压由下式确定：

　　（2-1-2）

　　表2：各种模块技术的PV *SOL®模型的标准值

　　模块技术ETL Emin k ffExtra

　　瓦/平方米瓦/平方米--

　　非晶硅150 2.2E-6 0.9685 1.03

　　碲化镉200 1E-7 1 1.03

　　非晶250 5E-8 1.03 1

　　独联体300 0.1 1 1.1

　　命中200 1E-7 1.04 1.04

　　所有其他300 0.1 1 1.05

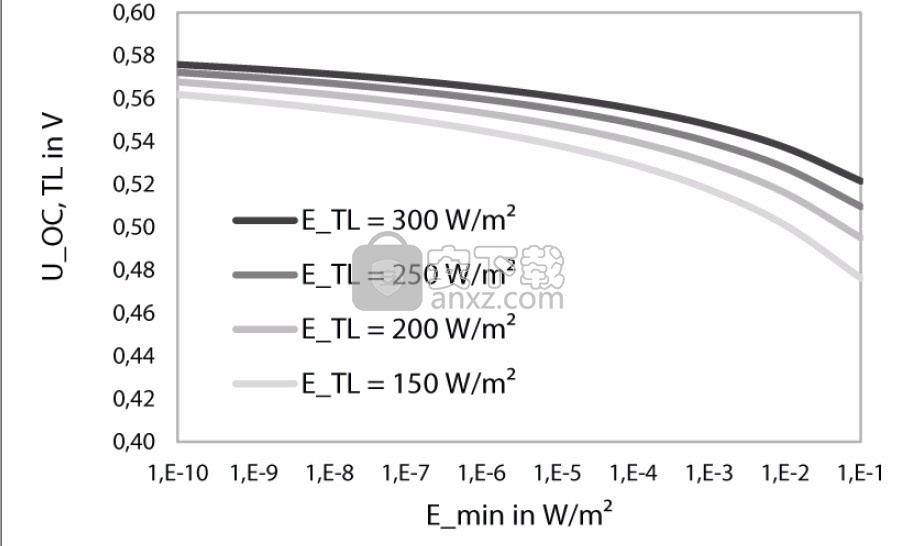
　　选择的Emin越小，ETL越大，则在部分负载点的空载电压下降幅度就越小（参见图4中的示例，UOC，STC = 0.6 V）。

　　图4：部分负载开路电压与Emin和ETL的关系。

　　如上所述，短路电流根据

　　MPP中的电流和电压最初设置为等于UMPP，TL = 1.1·UOC，TL和IMPP，TL = 0。以下是当前的等式

　　和紧张

　　在MPP中，以及用

　　重复直到UMPP，TL> UOC，TL或k> 2.一旦确定了部分负荷值，就可以针对每次辐照和温度计算它们了。

　　2.1.3。填充系数

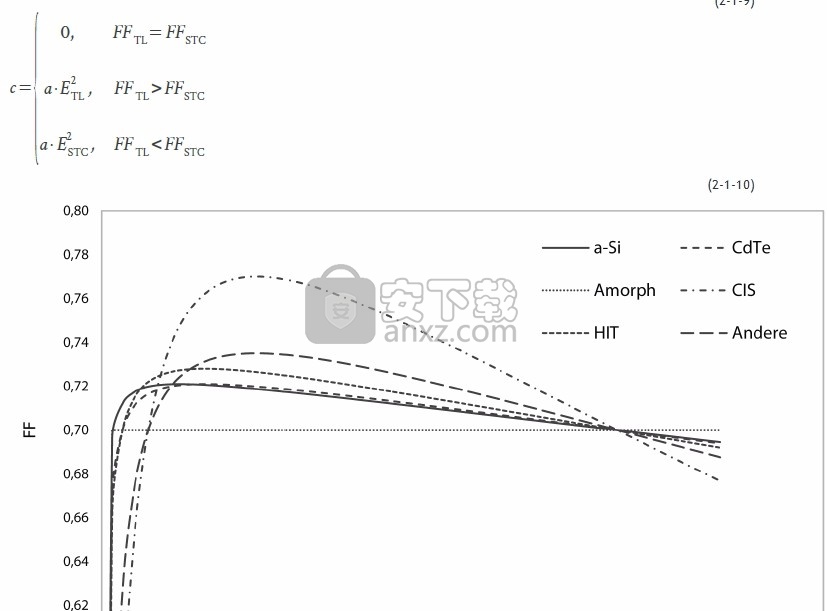
　　填充因子的特征行为现在由一个二次方程的逆表示，其中E对应于模块级的全局辐射：

　　系数a，b和c的计算方法如下，具体取决于部分负荷填充因子的大小：

　　图5：各种模块技术的填充系数与辐射的关系。

　　为了说明这一点，图5显示了取决于辐射的填充因子的不同曲线。对于所有技术，假定STC条件的虚拟填充因子均为0.7。

　　类似于根据公式（2-1-2）在部分负载点的计算，现在的空载电压为

　　进行计算，因此必须注意，此处必须在V / K中使用αU。辅助变量G0确保部分负载的空载电压为UOC，TL：

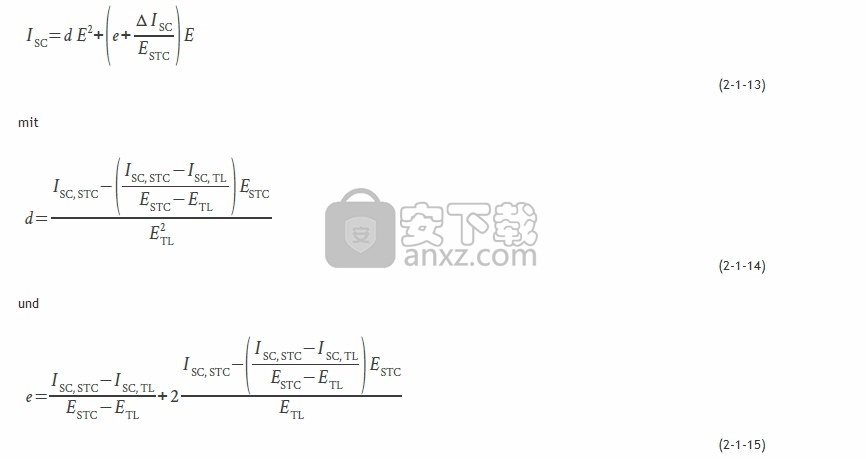
　　2.1.5。短路电流

　　现在根据电流辐照小于还是大于部分负荷辐照来计算短路电流。如果较低，则适用二次关系

　　温度依赖性溢出

　　进入计算（此处也必须使用绝对值，因此[αI] = A / K）。如果辐照大于部分负载点的辐照，则短路电流与辐照之间存在线性关系，所有模型都相同：

　　2.1.6。 MPP

　　MPP电流的计算也分为两个区域-对应于短路电流的计算。在0和部分负载点之间的辐照区域中，该规定适用

　　用

　　并且取决于功率αP的温度系数（这次是0到1之间的值）

　　ΔUOC的计算类似于电流：

　　如果辐照高于部分负载点，则可以在STC条件下简单地通过MPP与短路电流之比来缩放MPP电流，并获得

　　计算了短路，开路和MPP这三个参数。

　　在这些朋克之间特征曲线可以按指数插值。以下适用于短路和MPP之间的区域

　　用

　　逆函数（y）为函数的已知y提供x值的近似值

　　因为无法明确计算。

　　在第二个区域-MPP和空转之间-特征曲线近似如下：

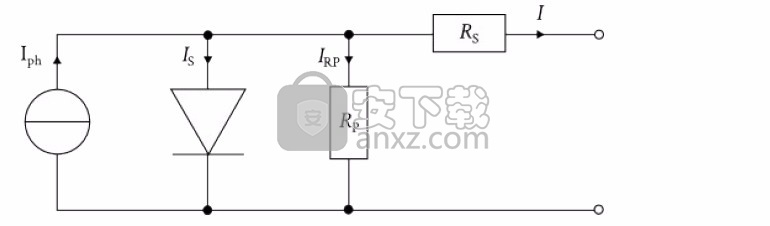
　　一二极管模型

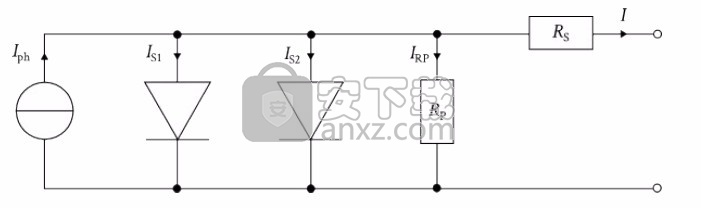
　　如果您展开光伏电池的等效电路图，该光伏电池由一个电源和一个并联且串联一个电阻的二极管并联而成，则您将获得单二极管模型的电路图：

　　图6：单二极管模型的等效电路图。

　　原则上，电流源对电子-空穴对的生成进行建模，该电子-空穴对通过p-n结中的电压分开，然后通过外部负载转移。 p-n结本身在电路图中由二极管表示。电子-空穴对例如在电池的边缘处发生的复合被并联电阻考虑，而串联电阻反映了通过接触，线等的损耗。

　　因此，可以在端子上以一定电压从电池中汲取的电流可以表示为SHOCKLEY方程的扩展：

　　因此，在STC条件下，光电流Iph总是略高于待测电流，因此略高于短路电流ISC，STC。它与辐射呈线性关系，并随着细胞温度的升高而增加：

　　参数C1和C2取决于单元和模块，但是可以很容易地至少大约从制造商的信息中计算得出。

　　饱和电流IS可以

　　可以更详细地描述，通常在10-11到10-9 A的数量级。取决于材料和技术的常数CS的值约为102 A / K3，温度κ的指数通常在文献中给出为3， EGap是电池材料的带隙（例如，室温下EGap，Si（T = 300K）≈硅的1.12 eV）。温度或热电压UT与

　　计算有时，二极管因子m包含在计算中。但最终，当然，单独查看二极管因数而不是作为热电压的一部分当然是等效的。从物理上讲，二极管因子应具有重组效应，并且A.在p-n转换中。在文献中，大多数情况下会设置m = 1，尽管所有细胞技术都显示出类似的重组行为值得怀疑。

　　最后，保留串联电阻RS和并联电阻RP来描述公式（2-2-1）中使用的公式符号。对于现代太阳能电池，电阻应在RS = 10-1Ω或RP = 102Ω的范围内。

　　可以假设串联电阻在很大程度上与辐射和温度无关，而并联电阻与辐射成反比。

　　边界条件

　　通常，在STC条件下，由数据表信息定义的四种情况可以根据特征方程式（2-2-1）描述如下。在空载运行中，电压采用数据手册上规定的开路电压UOC，STC的值，电流变为0：

　　在短路情况下，电压再次变为0，而电流采用数据表中的值：

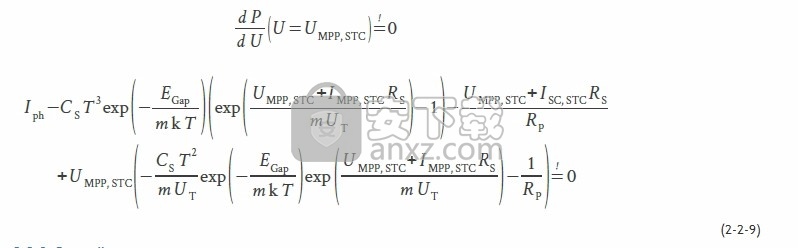
　　在最大功率（MPP）方面，还给出了电流和电压：

　　此外，MPP中的功率梯度必须为0。所以：

　　动力学

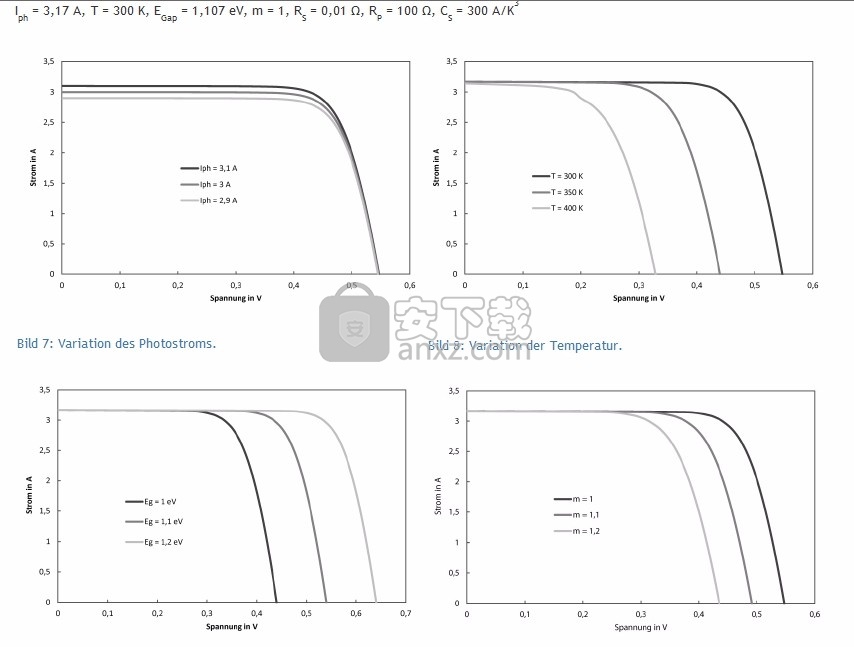
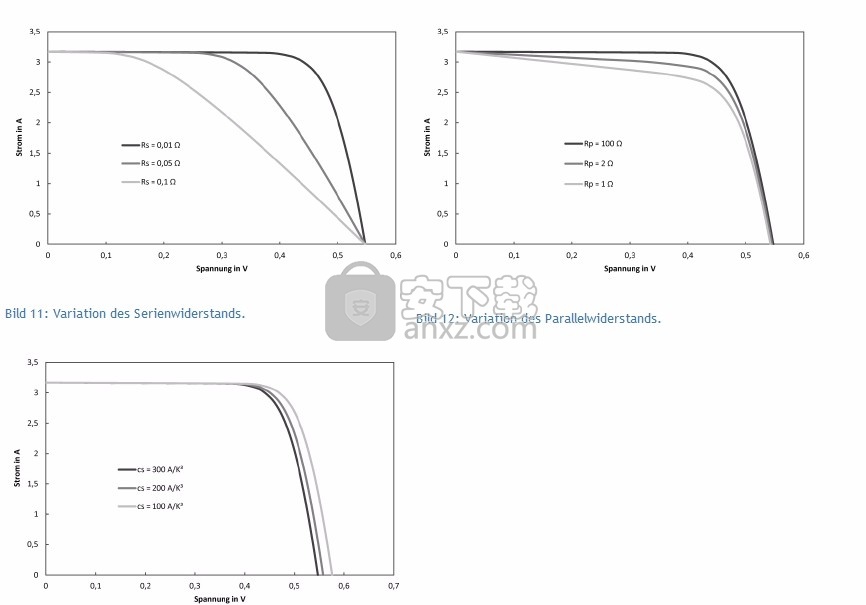
　　为了能够评估单二极管模型对各种参数的反应，下面显示了I-U特性，其中每种情况下一个参数都会变化。除非图中另有说明，否则参数定义如下：

　　Iph = 3.17 A，T = 300 K，EGap = 1.107 eV，m = 1，RS = 0.01Ω，RP = 100Ω，CS = 300 A / K3

　　参数确定

　　通常，光伏组件制造商的数据表仅提供STC条件下组件的基本电气数据。其中包括开路电压UOC，STC，短路电流ISC，STC，MPP UMPP，STC和IMPP，STC中的电压和电流，以及在大多数情况下的开路电压αU和短路电流αI的温度系数。

　　一二极管模型的参数可以从该信息中计算出来。

　　两二极管模型

　　两二极管模型增加了上述内容与单二极管模型中所述的第一个二极管并联添加了另一个二极管，这通常有助于提高MPP区域中的成像精度。

　　图14：两二极管模型的等效电路图。

　　因此，将另一项添加到特性的计算模型中。二极管因数m1和m2通常设置为等于1或2，并且饱和电流IS1和IS2的大小也不同。

　　根据等式（2-2-2），类似于单二极管模型计算光电流Iph。饱和电流超过

　　计算。指数κ1和κ2在文献中几乎一致地表示为3和5/2。因此，二二极管模型比一二极管模型包含更多的两个参数：二极管系数m2和饱和系数CS2。此外，还有一些方法质疑饱和电流方程中温度κ1和κ2的指数的精确值，并得出偏离3和5/2的值。

　　边界条件

　　可以类似于一二极管模型来设置四个边界条件。闲置方程

　　本质上，当参数变化时，两二极管模型的I-U特性与一二极管模型的行为类似。为了完整起见，此处显示了两个新参数的变体：

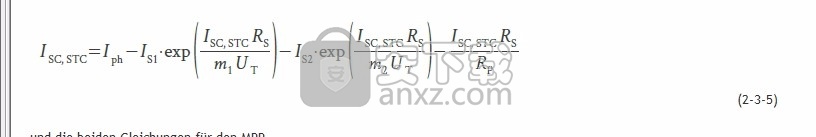
　　图15：第二个二极管系数的变化。

　　图16：第二饱和因子的变化。

　　可以看出，特性曲线对第二个二极管因数的反应比对第一个二极管因数的反应更不敏感。这样做的原因是，一方面，第二个二极管系数要比第一个二极管系数小几个数量级（CS2≈10-2A / K5 / 2），另一方面，在此期间温度会升高到较低的功率。

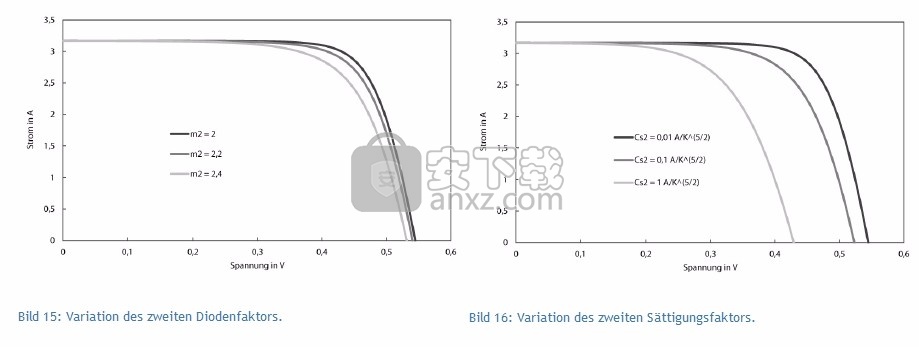
　　图17：第二个二极管项与第一个二极管项的影响。

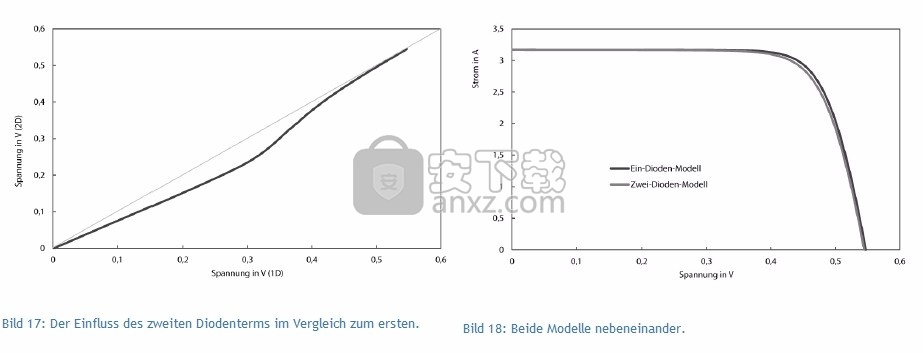
　　图片18：两种型号并排放置。

　　第二项如何精确地影响特性，如图17所示。将用两二极管模型计算的电压相对于用一二极管模型计算的电压作图。应当注意，第二个二极管项在MPP电压以下的区域中具有最明显的作用。但是，两二极管模型在短路点和开路点上没有提供任何偏差结果。图18同时显示了两个模型的I-U特性。

　　参数确定

　　在两二极管模型中，第二个二极管项在一个二极管模型中已经确定的参数上又增加了两个参数。

　　第二饱和因子CS2和

　　第二个二极管因数m2

　　因此，您得到的系统最初有八个未知数。由于在这种情况下也无法明确计算出带隙EGap和二极管因数m1和m2，因此将其替换为文献中的常规值。