ds simulia xflow 2019x

　　xflow2019x是索达公司开发的一款功能强大的流体仿真软件，新版本优化了基于粒子的动力学求解器：XFlow采用了一种新的基于粒子的动力学算法，可以解决玻尔兹曼和可压缩的Navier-Stokes方程，求解器具有最先进的大涡模拟（LES）建模和先进的非平衡墙模型；支持单一一致墙模型：XFlow使用统一的非平衡墙函数来模拟边界层，这种墙模型适用于所有情况，这意味着不必在不同算法之间进行选择并处理每种方案的不同限制；支持自适应尾流细化：XFlow引擎自动根据用户的要求调整分辨率，提高墙壁附近解决方案的质量，并在流量发展时动态适应尾流；内置高级建模功能：XFlow能够处理大型复杂模型，并通过移动部件，分层结构，强制或刚体运动以及接触建模大大简化分析设置；拥有先进的分析功能：XFlow求解器还具有热分析，共轭传热，跨音速和超音速流动，流经多孔介质，非牛顿流动以及复杂的边界条件，包括多孔跳跃和风扇模型。强大又实用，需要的用户可以下载体验

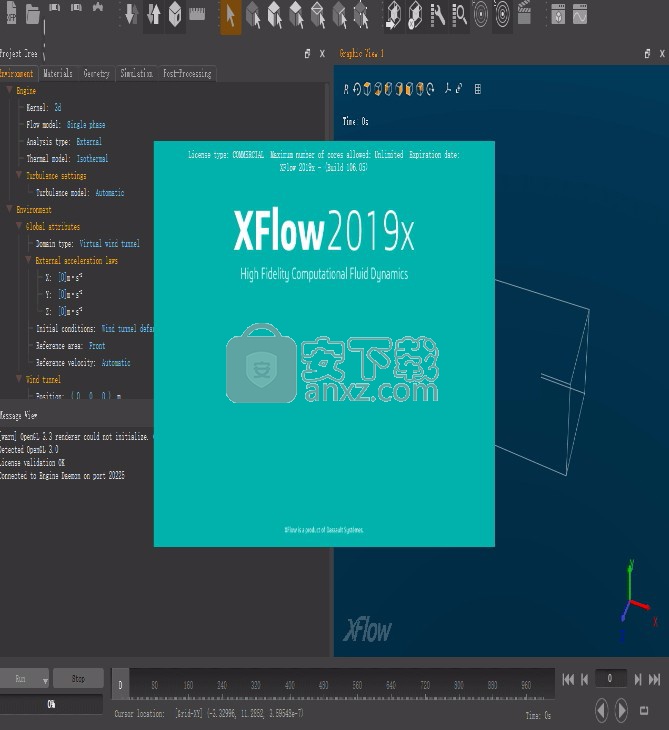
新版功能

　　1、在同一固体上应用体积热源边界条件和共轭传热（CHT）边界条件

　　2、增强的XFlow-Abaqus双向协同仿真功能

　　3、新的XFlow-Abaqus单向模拟能力，适用于小流体引起的结构变形

　　4、改进的任意参考框架，用于强制移动体的模拟

　　5、Power By增强功能可以将XFlow和仿真模型的数值结果上传到3D EXPERIENCE平台

　　6、增强的等值面可视化，用于具有多分辨率晶格域的仿真

　　7、使用新参数改进动画生成器以更好地控制输出动画文件

　　近线性可扩展性能：即使在标准台式PC上，XFlow也快速高效。它完全并行化，适用于具有近线性可扩展性的多核技术。

　　易于使用的界面：XFlow为用户提供独特而新颖的界面和工作环境，包括完全集成在同一环境中的预处理器，求解器和后处理器，最先进的可视化和可配置的布局。

软件特色

　　1、超越 Lattice Boltzmann 方法

　　在非均衡统计结构中，Boltzmann 等式可描述以中观比例建模的气体的行为。

　　Boltzmann 等式可以再现流体动力学限制，但是也能在航空航天、微流体或甚至是近真空条件等应用领域中对稀薄介质进行建模。

　　与标准 MRT 相反，XFlow 中的散射算符在中央矩空间中实施，可以自然提高代码的伽利略不变性、准确性和稳定性。

　　2、粒子型运动解算器

　　xflow2019x采用了一种新颖的粒子型运动算法，它经过特别设计，即使在普通的硬件配置下也能极快地执行。

　　xflow2019x中的离散化方法可避免一般的域网格化过程，并且曲面复杂性也不再是一种限制因素。

　　3、自适应点阵优化

　　xflow2019x引擎可以按照用户要求自动调整解算比例，从而优化壁面附近的解算质量，同时动态适应存在的强梯度并在流动形成时优化唤醒。

　　4、扰动建模：高保真度 WMLES

　　xflow2019x采用保真度极高的壁面建模大涡流仿真 (WMLES) 方法来执行扰动建模。

　　内在的先进 LES 方法基于壁面自适应局部涡流 (WALE) 粘度模型，提供了一致的局部涡流粘度和近壁面行为。

　　此外，它占用 CPU 的时间与仅提供 RANS 分析的大多数规范类似。

　　XFlow 使用统一的非均衡壁面函数对边界层建模。

　　安装步骤

　　1、用户只需要点击本网站提供的下载地址即可将应用程序下载到您指定的磁盘，得到对应的程序数据包，解药后即可使用

　　2、软件安装前，一定要删除以前的xflow版本，还要卸载干净，防止不能注册；

　　进入Crack\Server目录：

　　解压SSQ_UniversalLicenseServer_Core_20180127075000.zip

　　解压SSQ_UniversalLicenseServer_Module_NextLimitTechnologies_20180127075000.zip

　　复制Vendors到SolidSQUAD_License_Servers合并文件夹

　　3、复制SolidSQUAD_License_Servers到一个指定位置，比如放在C盘根目录下；

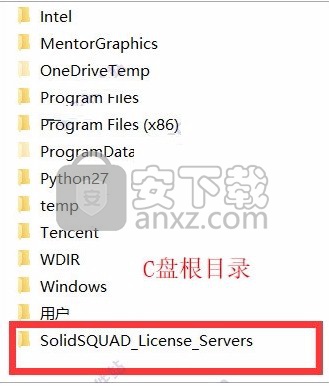
　　4、右键管理员身份运行install_or_update.bat；

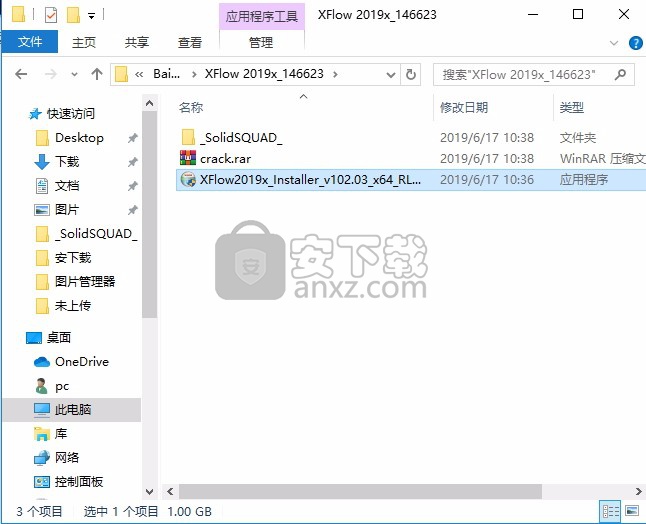
　　5、打开安装包，点击XFlow2019x_Refresh2_Installer_x64_RLM即可直接将应用程序点击进行安装

　　6、这个向导将指引你完成“XF1ow2019x”的安装进程。在开始玄装之前:建议先关闭其他所有应用程序。这充许“安装程序”重新指定的系统文件,而不需要重新启动你的计算机。单击[下一步()]继续。

　　7、Setup将安装XF1ow2019x在下列文件夹要安装到不同文件夹,单击[浏览(B)]并选择其他的文件夹。单击安装门开始安袭进程。（默认路径）

　　8、正在完成“X1ow2019x”已安装在你的系统。单击[完成()关闭此向导。

　　19、启动软件，如果要求许可文件服务器和端口，

　　name: localhost

　　port: 26800

　　10、完成以上操作步骤，即可将应用程序完成

使用说明

　　项目树包含文件夹和节点的层次结构，用户可以在其中轻松设置模拟参数。它分为五个类别，遵循执行CFD分析所需的逻辑顺序。

　　项目树窗口

　　项目树类别：

　　•环境：此类别包含两个主要文件夹：（a）引擎 - 选择XFlow引擎（+信息）; （b）环境 - 定义问题边界条件，初始解和外力（+信息）。

　　•材料：在此类别中，必须定义流体的热物理特性（+信息）。

　　•几何：几何对象显示在此数据结构中。这里，指定了对象行为和边界条件（+ Info）。

　　•模拟：在项目树（+ Info）的此分支中设置数值模拟的控制参数。

　　•后处理：运行模拟后，此处显示可视化和后处理选项（+信息）。

　　提示：要隐藏/显示项目树结构的所有文件夹和节点，请右键单击“项目树”窗口，将出现一个下拉菜单，其中包含以下选项：全部折叠;展开全部。

　　可以在以下位置自定义“项目树”窗口：

　　主菜单>选项>首选项>项目树（+信息），或设置

　　项目树中的可编辑字段具有以下类型：

　　1.下拉列表：单击符号以显示所有选项。

　　2.号码：点击号码进行更改。

　　3.开/关：单击开/关一词可在两个选项之间切换。

　　4.方括号[]：用户可以使用数字，函数，文件中的表格数据或字符串（例如几何对象的名称）来定义此类字段。 在括号内单击以使该字段可编辑。

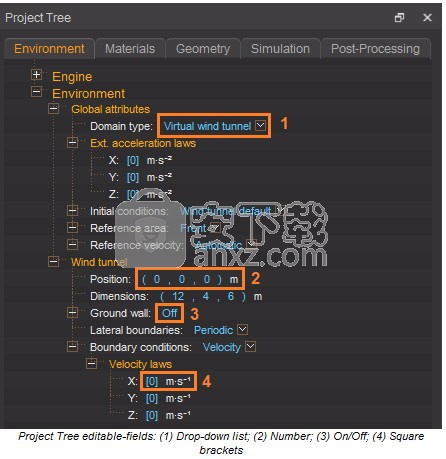
　　项目树可编辑字段：（1）下拉列表; （2）数量; （3）开/关; （4）方括号

　　请注意：输入字段接受科学记数法（例如0.00001 = 1e-05），小数必须用逗号表示（例如2.5，而不是2.5）。

　　提示：复制（Ctrl + C），剪切（Ctrl + X）和粘贴（Ctrl + V）的标准快捷方式可用于编辑项目树。

　　在项目树中，可以在方括号可编辑字段中定义函数。这些函数的语法应如下所示：

　　请注意：法律接受科学记数法（例如0.00001 = 1e-05），小数点必须用逗号表示（例如2.5，而不是2,5）。

　　提示：可以从下面显示的所有变量和函数创建用户定义的变量。

　　系统变量

　　通常，方括号字段可以定义为系统的以下变量的函数：

　　Ť

　　时间

　　X

　　空间坐标

　　ÿ

　　空间坐标

　　ž

　　空间坐标

　　PI

　　号码pi

　　VX（X，Y，Z）

　　域的离散点处的速度的x分量，由坐标（x，y，z）给出

　　VY（X，Y，Z）

　　域的离散点处的速度的y分量，由坐标（x，y，z）给出

　　VZ（X，Y，Z）

　　域的离散点处的速度的z分量，由坐标（x，y，z）给出

　　VMOD（X，Y，Z）

　　域的离散点处的速度幅度，由坐标（x，y，z）给出

　　SP（X，Y，Z）

　　域的离散点处的静压，由坐标（x，y，z）给出

　　U（X，Y，Z）

　　域的离散点处的温度，由坐标（x，y，z）给出

　　请注意：评估速度或静压的离散点的坐标也可以定义为函数，例如：vx（sin（t），0,0）。

　　此外，对于后处理使用，可以将自定义字段定义为以下变量的函数：

　　SP

　　静压力

　　RHO

　　参考密度

　　VMOD

　　速度模块

　　VRT

　　涡

　　比照

　　皮肤摩擦系数

　　TI

　　湍流强度

　　TP

　　总压力

　　ü

　　温度

　　粘性

　　有效粘度

　　NX

　　表面法线的x分量

　　纽约

　　表面法线的y分量

　　新西兰

　　表面法线的z分量

　　请注意：“rho”表示在项目树>材料>流体>密度中定义的参考密度，因此它是一个常数值。

　　如果是具有两个相的自由表面流（项目树>材料>流体>两相模型：打开），“rho”将返回第一阶段的参考密度（项目树>材料>流体>密度）。

　　对于刚体动力学实体，以下变量可供用户使用：

　　px，py，pz

　　在X，Y和Z方向上的位置

　　vx，vy，vz

　　X，Y和Z方向的速度

　　ax，ay，az

　　X，Y和Z方向的加速度

　　eux，euy，euz

　　X，Y和Z方向的旋转角度

　　wx，wy，wz

　　X，Y和Z方向的角速度

　　对于非等温情况和非牛顿用户定义的流体，用户还可以访问温度变量：

　　theta（θ）

　　温度

　　对于非牛顿用户定义的流体，流体的粘度可能取决于剪切速率：

　　伽玛（）

　　剪切率

　　在多阶段情况下：

　　VOF

　　液相体积

　　使用离散相模型（DPM）时，可以区分流体和粒子系统变量，如下所示：

　　particle_x

　　particle_y

　　particle_z

　　粒子在X，Y和Z方向上的位置

　　particle_vx

　　particle_vy

　　particle_vz

　　X，Y和Z方向的粒子速度

　　particle_t

　　粒子时间

　　particle_vN

　　与固体碰撞时的粒子法向速度

　　particle_vT

　　与固体碰撞时的粒子切向速度

　　particle_vNDrift

　　与固体碰撞时的粒子漂移法向速度

　　particle_vTDrift

　　与固体碰撞时的粒子漂移法向速度

　　particle_diam

　　粒径

　　fluid_px

　　fluid_py

　　fluid_pz

　　X，Y和Z方向的流体位置

　　fluid_vx

　　fluid_vy

　　fluid_vz

　　X，Y和Z方向的流体速度

　　fluid_sp

　　流体静压

　　fluid_vrt

　　流体涡度

　　在FMI标准中：

　　FMU（）

　　FMU计算的输入变量

　　算术运算符：

　　函数可能涉及算术运算，例如：提升权力

　　标量函数：

　　标准标量函数也可用：

　　SQRT（x）的

　　平方根

　　EXP（x）的

　　指数

　　日志（X）

　　对数

　　（基础e）

　　日志10（x）的

　　对数

　　（基数10）

　　ABS（x）的

　　绝对值

　　的sin（x）

　　正弦

　　（弧度为x）

　　COS（x）的

　　余弦

　　（弧度为x）

　　棕褐色（x）的

　　切线

　　（弧度为x）

　　ASIN（x）的

　　反正弦

　　（弧度为x）

　　ACOS（x）的

　　反余弦

　　（弧度为x）

　　ATAN（x）的

　　反正切

　　（弧度为x）

　　RND（x）的

　　随机

　　（0到x之间的随机数）

　　地板（X）

　　地板

　　（最大整数小于或等于x）

　　小区（x）的

　　小区

　　（最大或等于x的最小整数）

　　J0（x）的

　　贝塞尔函数j0

　　J1（x）的

　　贝塞尔函数j1

　　插值函数：

　　连续函数可以通过离散点插值定义，如下所示：

　　linearinterpolation（t; {t_0，value_0}; {t_1，value_1}; ...; {t_n，value_n}）

　　离散点的线性插值

　　cubicinterpolation（t; {t_0，value_0}; {t_1，value_1}; ...; {t_n，value_n}）

　　离散点的立方插值

　　其中t代表任何自变量（x，y，z，t）。

　　条件陈述：

　　if（condition，statement1，statement2）

　　如果condition为“true”：它返回statement1，否则：它返回statement2。

　　有效的关系运算符：>，<

　　在条件中表达逻辑关系

　　如果[（x> 0），1,0]

　　它返回一个步长函数，步长为1，x = 0

　　如果[（x> 0）（x <1），1,0]

　　它返回一个boxcar函数，x的值为1，介于0和1之间

　　如果[（（x> 1）+（x <0）），1,0]

　　x> 1时为1，x <0时，x为0，介于0和0之间

　　请注意：如果算术运算等于零，则语句为FALSE，否则为TRUE。

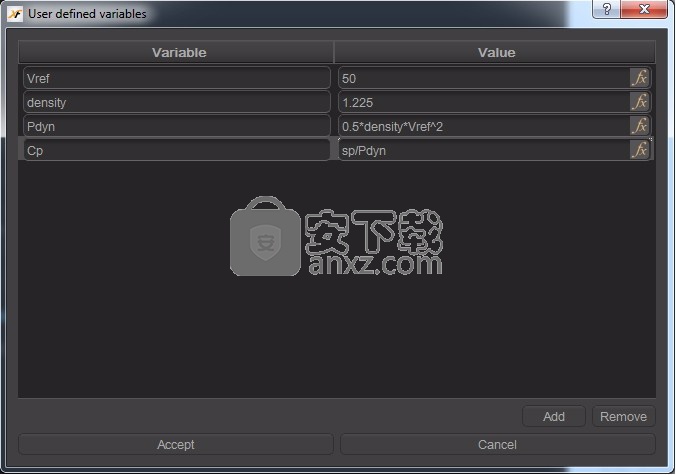
　　可以创建用户定义的变量以用于模拟设置以及后处理。它们对参数化项目非常有帮助，例如，仅在一个地方修改多个输入中使用的变量的值。

　　主菜单>选项>用户定义的变量

　　窗口分为两列：左侧的变量名称和右侧的变量值。要添加新的用户定义变量，请单击“添加”，将显示一个新的空行。您可以通过单击“删除”删除任何用户定义的变量。为每个项目定义用户变量，并将其保存在XFlow项目文件中。函数章节中定义的所有函数和变量都可以在变量定律中使用。

　　请注意：必须考虑一些重要细节：

　　1.产品“*”应明确写入法律。

　　2.可以使用另一个用户定义的变量定义用户定义的变量，但是定义是有序的，必须首先定义其他变量调用的变量。

　　3. XFlow中定义的函数不能用作变量名。

　　4.变量名称不区分大小写。例如，Cp = CP = cp = cP。

　　定义压力系数Cp的示例如下图所示：

　　XFlow允许用户通过从文本文件（.txt，.dat）中读取表格数据来使用方括号[]填充可编辑字段。有三种选择：

　　没有插值

　　tabulardata（indep_variable_1，...，indep_variable_n，“path \ file.dat”）

　　线性插值

　　tabulardatalinearinterpolated（indep_variable_1，...，indep_variable_n，“path \ file.txt”）

　　立方插值

　　tabulardatacubicinterpolated（indep_variable_1，...，indep_variable_n，“path \ file.txt”）

　　Sinc插值

　　tabulardatasincinterpolated（indep_variable_1，...，indep_variable_n，“path \ file.txt”，order）

　　其中“indep_variable_1”或“indep_variable_n”代表以下任何变量：

　　Ť 时间

　　X空间坐标

　　ÿ

　　空间坐标

　　ž

　　空间坐标

　　px，py，pz

　　在X，Y和Z方向上的位置

　　vx，vy，vz

　　X，Y和Z方向的速度

　　下表显示了文本文件的语法示例：

　　☞示例：file.txt或file.dat

　　// 评论

　　// x y值

　　0.1 1.4 0

　　2.3 -1.7 1

　　-5.5 3.8 0

　　要读取此文件，语法将为：tabulardata（x，y，“path \ file.txt”）或tabulardata（x，y，“path \ file.dat”）

　　请注意：表中的最后一列始终是输出值。函数的独立变量不需要按文本文件中的值排序。路径和文件名必须用引号括起来。

　　提示：函数的独立变量可以是系统变量的函数。

　　示例：tabulardata（2 * x，“complete_route \ file.txt”）

　　提示：在带括号的字段中，可以使用表格数据给出的函数进行操作。这允许用户轻松地重新缩放数据。示例：[10 * tabulardata（2 * x，“complete_route \ file.txt”）]

　　没有插值

　　语法如下：

　　tabulardata（indep_variable_1，indep_variable_2，...，indep_variable_n，“path \ file.txt”）

　　它为每个计算元素分配表中最接近的值。

　　线性插值

　　语法如下：

　　tabulardatalinearinterpolated（indep_variable_1，...，indep_variable_n，“path \ file.txt”）

　　XFlow可以线性插值表格数据文件的每个点之间的结果。

　　立方插值

　　语法如下：

　　tabulardatacubicinterpolated（indep_variable_1，...，indep_variable_n，“path \ file.txt”）

　　XFlow可以使用三次多项式函数在表格数据文件的每个点之间插值结果。

　　Sinc插值

　　语法如下：

　　tabulardatasincinterpolated（indep_variable_1，indep_variable_2，...，indep_variable_n，“complete_route \ file.txt”，order）

　　XFlow还可以从具有“sinc”函数（sinc（X）= sin（X）/ X）的文件中插入表格数据，其中“order”参数是在插值内核中使用的采样点的数量。 sinc功能。此“order”参数可以取3到表格数据文件中可用值的最大值之间的值。

　　Sinc功能

　　请注意：“order”参数越高，插值就越准确。然而，如果该参数非常高，则可以观察到计算成本。

　　如果在任何树的空白区域中右键单击（鼠标右键），将显示一个下拉列表，它显示树管理选项：

　　•全部折叠：重新排列树以仅显示根

　　•全部展开：重新排列树以显示其部署的所有元素

　　如果树中的任何可用对象都有一个复选框，则下拉列表还将显示：

　　•设置所有选定的可见：这将勾选所有选定的对象

　　•设置所有选定的不可见：这将取消选中所有对象

　　•设置全部可见：这将勾选当前树中的所有对象

　　•设置所有不可见：这将取消当前树中的所有对象消息视图对于跟踪计算进度特别有用，因为它为每个求解器迭代显示以下信息：

　　•Sim.Time（模拟时间）

　　•稳定性参数。 （稳定性参数）

　　•挂钟时间

　　•Num elems（元素数量）

　　模拟时间

　　它是已经模拟的物理时间总量。换句话说，它是到目前为止计算的时间步长的增加。

　　稳定性参数

　　稳定性参数允许用户检查溶液稳定性。稳定性参数定义为：

　　稳定性参数必须满足Courant-Friedrichs-Lewy（CFL）条件，因此其值必须小于1.如果达到1.0，则意味着CFL中的某个地方不满足，模拟的稳定性是因此无法确保，XFlow在消息视图中显示以下消息：

　　“[警告]稳定性参数太高，请检查（X，Y，Z）m处的[压力/速度/粘度]或缩短时间步长。”。

　　在这种情况下，用户应停止模拟，减少时间步长并再次开始计算。

　　稳定性参数的值可以在功能查看器中以图形方式显示。

　　请注意：启用超音速热模型后，稳定性参数不可用。

　　提示：建议将稳定性参数保持在0.1-0.3左右

　　挂钟时间

　　它是引擎计算时间步长所需的实时量。此时间可能受XFlow以外的外部应用程序的影响，并且不仅代表CPU时间，而且仅代表实际的挂钟时间。

　　元素数量

　　如果晶格的拓扑不固定，即启用细化算法自适应细化，则域中元素的数量将随时间变化。仅在这种情况下，每个求解器迭代中的元素数量都显示在消息视图中。

　　☞示例：消息视图输出

　　域生成器（generateDomain3d.exe）首先创建流体域。这些消息保存在pre_processor.log文件中（请参阅XFlow文件）：

　　## DOMAIN GENERATION ##

　　XFlow Build 98

　　执行行：C：\ Program Files \ Next Limit \ XFlow \ generateDomain3d.exe Project.xfd -log = 2 / maxcpu = 4

　　计算仅限于：4核。

　　RLM许可证验证确定

　　Num cpus检测到：4

　　生成具有3个级别的八叉树。

　　0级

　　1级

　　2级

　　确定晶格/几何交叉点......

　　用流体确定区域

　　自动确定带有流体的区域

　　1个丢弃的区域

　　1个确定的区域

　　生成节点映射。

　　0级的Num活动元素：119168/125000

　　第1级的数字活动元素：24704/46656

　　2级的Num活动元素：111616/175616

　　元素总数：255488

　　写域名

　　数字边界元素：10088

　　整体断开链接：87848

　　域已成功生成。

　　退出代码：[0 :: 0]

　　解算器（engine-3d * .exe）现在启动并通过加载生成的流体域进行预处理。以下所有消息都保存在project_name.log文件中（请参阅XFlow文件）：

　　##模拟开始##

　　XFlow Build 98

　　执行行：C：\ Program Files \ Next Limit \ XFlow \ engine-3d.exe Project.xfb / maxcpu = 4 -log = 2

　　计算仅限于：4核。

　　RLM许可证验证确定

　　Num cpus检测到：4

　　分配记忆......

　　数量级别：3

　　等级：0

　　Num活动流体元素：119168

　　1级

　　Num活动流体元素：24704

　　等级：2

　　Num活动流体元素：111616

　　处理几何...

　　完成！

　　完整域名有255488个元素。

　　等效单分辨率域有8000000

　　等效单分辨率域大小为（200 x 200 x 200）

　　求解器设置边界条件，估计主要参考值和时间步长：

　　计算边界条件图！

　　最粗分辨长度：0.2

　　普朗特数：0.180259

　　参考面积：3.99219平方公尺

　　参考速度：5米/秒

　　时间步长（0级）：0.001秒

　　求解器初始化流体域并保存初始模拟帧（第0帧）：

　　保存数据......

　　[[数据文件]] 0完成!!! |帧挂钟时间[0] s |总挂钟时间[0] s |数字[255488]