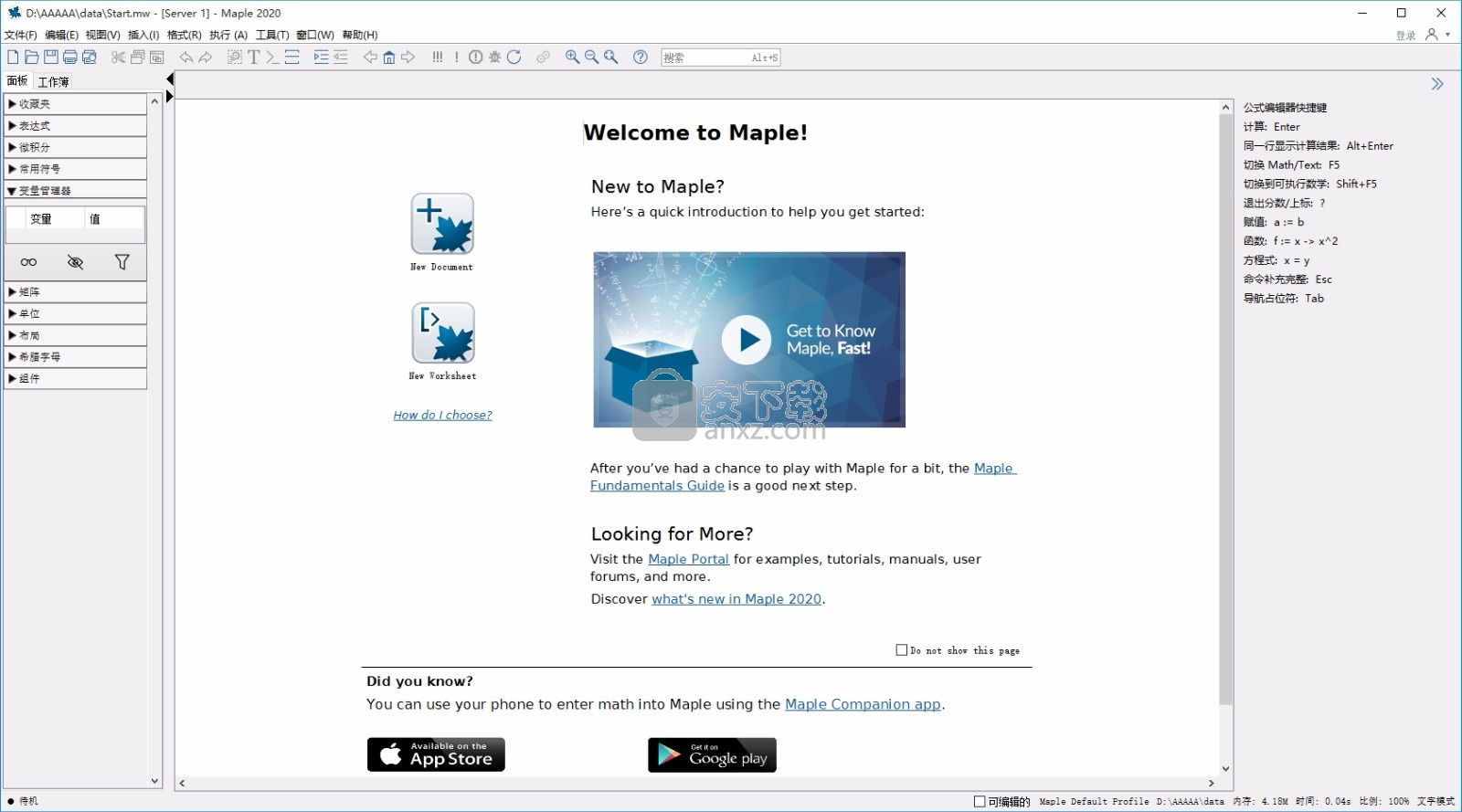
maple2020补丁-maplesoft maple 2020补丁下载附带安装教程

　　maple2020补丁是一款针对maplesoft maple 2020而开发的激活工具，可以直接将刚发布的应用程序进行完美激活，激活后就可以免费永久使用；新版本支持虚拟模拟，物理验证，与通过单独的硬件进行测试相比，仿真使学生能够安全地研究更大范围的条件，而不会损坏设备，且成本更低；编程工具更新，执行跟踪的改进；tracelast命令现在可以查看过去捕获并重新抛出的异常，当捕获并重新抛出异常时，该错误被报告为发生在包含catch子句的过程中；tracelast生成的堆栈跟踪现在将包括所有执行级别，直到最初发生错误为止；提供新的调试器命令，新的调试器命令help将显示所有调试器命令及其选项的简明摘要，该命令后可以跟一个可选主题，以仅显示与该主题有关的命令子集，在调试器中执行帮助gdb将显示从GNU调试器到Maple调试器命令的交叉引用；新的retstep命令类似于现有的return命令，不同之处在于执行在当前过程返回后在任何执行的语句处停止，而不是在调用过程中执行的下一条语句处停止；需要的用户可以下载体验

软件功能

　　1、支持任意精度的符号和数值计算

　　2、基本和特殊的数学函数库

　　3、复数和区间运算

　　4、有理数，有限域，代数数域和代数函数域上的多元多项式的算术，最大公约数和分解

　　5、微分代数

　　6、矩阵操作工具，包括对稀疏数组的支持

　　7、数学函数图形和动画工具

　　8、方程组，丢番图方程，ODE，偏微分方程，DAE，DDE和递归关系的求解器

　　9、用于离散和连续微积分的数字和符号工具，包括确定和不定积分，有限和无限求和，自动微分和连续和离散积分变换

　　10、受约束和不受约束的局部和全局优化

软件特色

　　1、统计包括模型拟合，假设检验和概率分布

　　2、用于数据处理，可视化和分析的工具

　　3、概率和组合问题的工具

　　4、支持时间序列和基于单位的数据

　　5、连接到在线收集财务和经济数据

　　6、财务计算工具，包括债券，年金，衍生品，期权等

安装步骤

　　1、用户可以点击本网站提供的下载路径下载得到对应的程序安装包

　　2、只需要使用解压功能将压缩包打开，双击主程序即可进行安装，弹出程序安装界面

　　3、同意上述协议条款，然后继续安装应用程序，点击同意按钮即可

　　4、可以根据自己的需要点击浏览按钮将应用程序的安装路径进行更改

　　5、弹出以下界面，用户可以直接使用鼠标点击下一步按钮

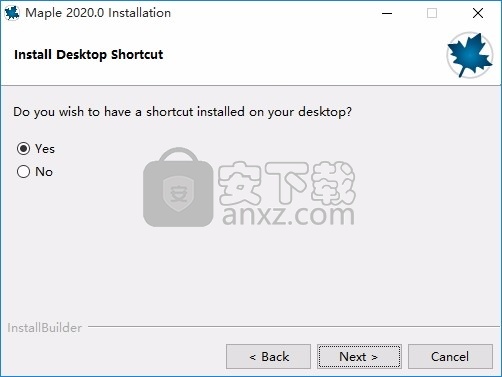
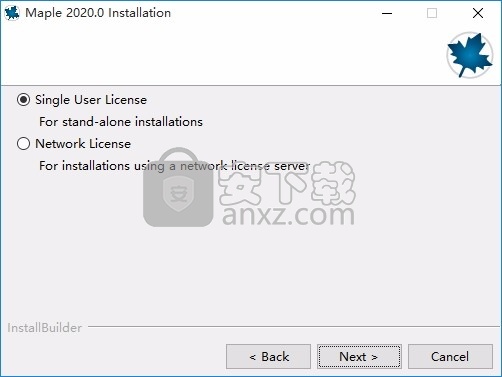
maple2020补丁

　　6、桌面快捷键的创建可以根据用户的需要进行创建，也可以不创建

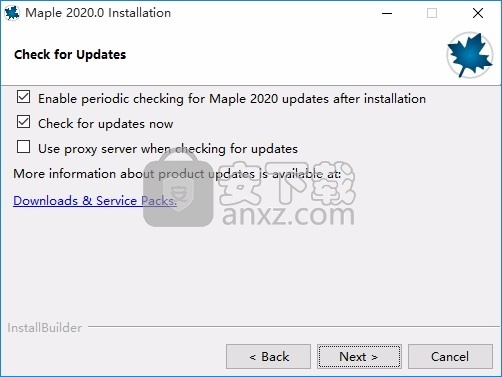
　　7、现在准备安装主程序，点击安装按钮开始安装

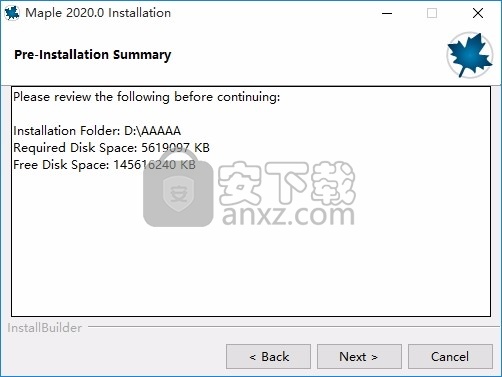
　　8、弹出应用程序安装进度条加载界面，只需要等待加载完成即可

　　9、根据提示点击安装，弹出程序安装完成界面，点击完成按钮即可

方法

　　1、程序安装完成后，先不要运行程序，打开安装包，然后将文件夹内的文件复制到粘贴板

　　2、然后打开程序安装路径，把复制的文件粘贴到对应的程序文件夹中然后运行，点击patch

　　C:\Program Files\Maple 2020\bin.X86_64_WINDOWS

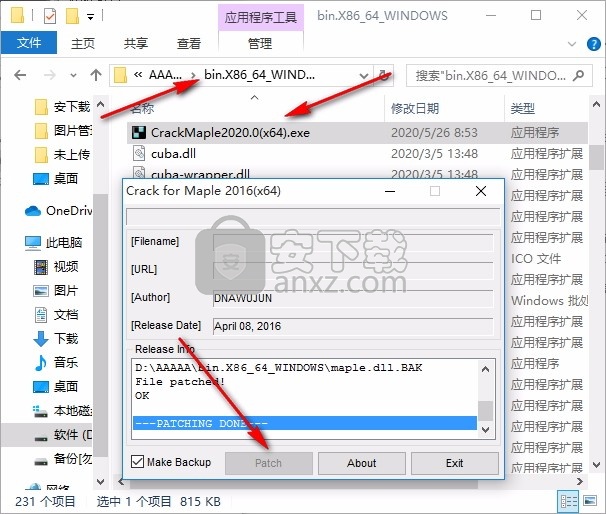
　　3、然后再将license文件夹内的license.dat复制到软件许可证目录下

maple2020补丁

　　4、完成以上操作步骤后，就可以双击应用程序将其打开，此时您就可以得到对应程序

使用说明

　　代码工具：-程序分析：-StaticCallGraph

　　StaticCallGraph返回一个有向图，该有向图表示输入P的静态调用图。该图的顶点是表示过程或适用模块的字符串，并且当体内显式引用g时，从f到g存在有向弧。的

　　输出是适合与GraphTheory包中的命令一起使用的Maple图。

　　ListTools：-切片

　　ListTools包中的Slice命令将一个列表切成一系列的子列表。子列表的数量由用户提供，序列中子列表的长度最多相差一个。请注意，如果指定的子列表数大于原始列表中的元素数，则结果是一系列由单个元素组成的子列表，后跟空列表。例如：

　　with（ListTools）;

　　为了进行比较，LengthSplit命令会根据目标长度拆分列表，该命令通常会返回长度相差较大的子列表

　　工作表程序包包含两个新命令：RemoveSection用于从Maple文档中删除所有节，而TableOfContents用于将节标题添加到Maple文档的开头。

　　URL [Download]具有用于指定证书文件，身份验证密码，代理和代理密码，超时等的新选项。

　　Iterator程序包包含有关de Bruijin序列，Lyndon单词，项链和项链的新命令，并且扩展了用于实现多重组合和有界构图的对象的Number方法。

　　向量场包的李代数

　　Maple 2020包括一个用于处理矢量场的李代数的新程序包，即面向对象的LieAlgebrasOfVectorFields程序包。该前沿软件包提供了一种探索Lie对称群性质的新方法。

　　当关于对称性线性化时，李对称组产生与一个参数组轨道相切的矢量场的李代数。这种线性化产生了矢量场的李代数分量的线性齐次PDE（LHPDE）的确定系统。

　　LieAlgebrasOfVectorFields软件包使用微分减少和消除算法从矢量场的这种Lie代数的确定系统中找到代数（例如中心，下中心级等）和几何（例如分布，不变式等）属性。它基于Lisle和Huang（2017）和Huang（2015）的结果。

　　此程序包是对DifferentialGeometry的补充，特别是DifferentialGeometry中的LieAlgebras程序包可以灵活地表述应用程序中出现的几何问题，使用户可以在使用外部微分系统和移动框架的同时在相关歧管上进行固有工作，从而制定并解决这些问题。微分几何还提供了广泛的教程和课程集，以帮助向软件包中介绍新用户。

　　与现有方法相反，LieAlgebrasOfVectorFields包强调了结构，几何和代数信息的早期开发，同时延迟了集成。并且在应用时确实在集成阶段利用了Maple现有的非常强大的pdsolve和dsolve功能。 LieAlgebrasOfVectorFields在集成和结构化方法的整个范围内提供了扩展的方法灵活性。这为用户提供了一种用于计算对称结构的有效替代方法，并且可以用作初步分析来确定是否存在诸如大而有趣的（例如可解）对称代数之类的合意特征，这些特征需要对已经在中实现的强大，更明确的基于解决方案的方法进行投资。枫。

　　在这里，我们在N个空间维度中使用一次Schrodinger量子力学方程，并用一次谐波谐振器势和时间相关系数来说明LAVF在更大计算量下的能力。这样的高维系统经常自然地出现。它是一个丰富的类，因为它包含一些简单的经典PDE，例如零电位Schrodinger方程，以及具有较大对称代数的物理上显着的谐振子电位。

　　以下命令序列设置了空间尺寸N（用户可以根据需要更改），然后设置时间相关的归一化薛定inger方程，通过更改a（t），b（t）和c（t ）（给出了a（t），b（t）和c（t）的3组值，最后一个是后续计算中使用的值）。

　　带有I7处理器和8 GB RAM的笔记本电脑大约需要2秒钟来计算给定示例的结构，其中N = 3，得出13维李代数。对于N = 10，相同的示例花费大约100秒，以计算N = 10的示例的结构，从而生成69维Lie代数。

　　进一步的探索性计算是：

　　这里的true表示存在变量的可逆变化，该变化将非线性ODE映射到线性ODE。 IsLinearizable是一个很好的例子，说明了LAVF如何有效地计算几何信息（在这种情况下为线性化图），以确定是否可以对问题应用更昂贵的方法（在这种情况下确定线性化）。

　　在这里，我们显示简单的过程，该过程使用LAVF命令，SymmetryLAVF，SolutionDimension，DerivedAlgebra和IsAbelian。

　　showstat（IsLinearizable）;

　　在上面的过程中，对于我们的示例，n =3。SymmetryLAVF设置矢量场的李代数，而m是李对称代数的维数m = 4 = n + 1。 LAVF指令IsAbelian（Da）得出true，而未确定派生代数Da的基础。基于Da初始数据空间上的诱导李代数，只需对Da的确定系统进行算法区分和消除。

　　实际上，Lyakhov，Gertt和Michels（2017）现在将LAVF用作其更昂贵的方法的有效先驱，这些方法使用对非线性映射方程的微分消除与pdsolve相结合来整合其简化形式并明确确定映射。

　　这些方法产生线性化为[z = u ^ 2 + x ^ 2，v = -x];

　　目标线性ODE在哪里“ diff（v（z），z，z，z）= -v（z）*（z +1）/ z”

　　参考文献

　　D.A.利亚霍夫（V.P.）盖特（Derg）和D.L.米歇尔斯（2017）。常微分方程线性化的算法验证。 Proc ISSAC 2017。

　　I.G.莱尔和S.-L.T.黄（2017）。李确定系统的算法演算。符号计算杂志。第79卷，P2：482-498。

　　S.-L.T.黄（2015）。基于李确定系统的矢量场的李代数的性质。堪培拉大学博士学位论文。

　　I.G.莱尔（G.J.里德（1998）。无限小定义系统中李伪群的几何和结构。 J.Symb。计算26（3）：355-379。

　　涉及“ e”和“ d”的常见错误警告

　　常见的新用户错误是，在引用指数常量时只需键入“ e”，而不是输入符号

　　或使用exp函数。枫认为

　　作为变量，会导致用户无法预期的结果，并且新用户可能难以诊断。使用变量时可能会发生类似情况

　　代替差异

　　Maple 2020现在可以检测到这种情况似乎正在发生的情况，并提供适当的警告和解决方案。

　　在文档和工作表模式之间选择

　　在“开始”页面上，要求用户在打开“新文档”和“新工作表”之间进行选择。现在，通过添加“如何选择？”更容易做出此选择。链接，概述每种模式的不同用例。这些信息将帮助新用户信心十足地做出初始选择，还将为他们提供知识，这些知识将指导他们在使用Maple时使用最合适的模式。

　　首页

　　Maple中更新的“开始”页面使新用户可以更轻松地为使用Maple的第一步找到最佳资源。更改包括：

　　更新的快速认识枫木！视频，其中提供了简短的概述和关键信息，以帮助所有用户进行首次Maple交互

　　修订的《 Maple基础知识指南》涵盖了更多主题，并包含有关在工作表模式下工作时的差异的信息。

　　简化的演示文稿清楚地指出了Maple新手的最重要资源

　　如上一节所述，协助在“文档”和“工作表”模式之间进行选择

　　您可以单击Maple中的许多错误和警告消息来访问网页，该网页更详细地说明了在什么情况下可能发生错误，以及解决该问题所需采取的措施。对于Maple 2020，更多错误消息具有帮助页面，可帮助您更快地诊断并从错误中恢复。

　　重新激活您的许可证

　　一些客户开始使用具有时间限制的许可证的Maple，包括许多在获得学生身份确认之前获得临时Maple许可证的学生。这些客户需要重新激活其Maple许可证才能继续使用Maple。现在，重新激活过程更简单。 Maple 2020在About Maple ...窗口中包括一个Reactivate License按钮，因此您不再需要运行单独的实用程序或等到许可证过期后再进行激活。

　　常微分方程和偏微分方程

　　枫树公司（Maple）在寻找普通和偏微分方程的精确解方面处于世界领先地位。

　　Maple 2020扩展了解决新ODE和PDE的新算法和技术，从而进一步领先，其中包括一般解决方案以及具有初始条件和/或边界条件的解决方案。

　　对于Maple 2020，无论有无初始条件或边界条件，对于ODE和PDE的精确解决方案，dsolve和pdsolve都有显着改进。

　　对于ODE，一种用于计算超几何解的新算法

　　“ 2 ^ nd”

　　阶线性ODE能够解决以前无法解决的新问题。

　　对于PDE，改进包括显着扩展的解决边界和初始条件问题的能力（还使用积分Mellin和Hankel变换）以及两种新的查找通用PDE解的方法，方法是将PDE映射到具有辅助功能的ODE并通过分解变成第一整数同样，当PDE依赖参数时，新的对称技术可让您计算参数化的对称性并减少这些参数的数量，这在不同情况下通常很方便。

　　二阶线性ODE的超几何解

　　Maple以前的版本已经具有用于计算线性ODE的超几何解决方案的算法。但是，在Maple 2020中实施的新算法更为通用。假设ODE接受以下形式的解决方案

　　是其他一些线性ODE的解决方案。然后，新算法可以计算其他线性ODE并将其求解，只要它接受以下形式的解

　　Y（x）= exp（int（r（x），x））*超大数（[a，b]，[c]，f（x））;

　　是x的有理函数，

　　“`#mscripts（mi（” F“），none（），none（），none（），none（），mn（” 2“），none（））`\

　　[1]”

　　是超几何函数，并且a，b和c是任意常数。新算法使用模块化归约，Hensel提升，有理函数重构和有理数重构。

　　该算法比以前的算法更具通用性，因为它对回调函数的程度没有任何限制

　　也不是输入方程的奇数。该实现遵循Imamoglu，E.和van Hoeij，M.的演讲“使用形式解和整数基商计算二阶线性微分方程的超几何解”，符号计算学报，83，（2017）：254-271 。

　　VectorCalculus和MultivariateCalculus软件包中的集成

　　现在，VectorCalculus和MultivariateCalculus程序包（以及相应的Student子程序包）中的集成命令使用折叠形式而不是嵌套形式进行多重集成。这允许外部集成步骤使用内部集成步骤的范围并从中直接受益。