Photon(函数图像生成器)

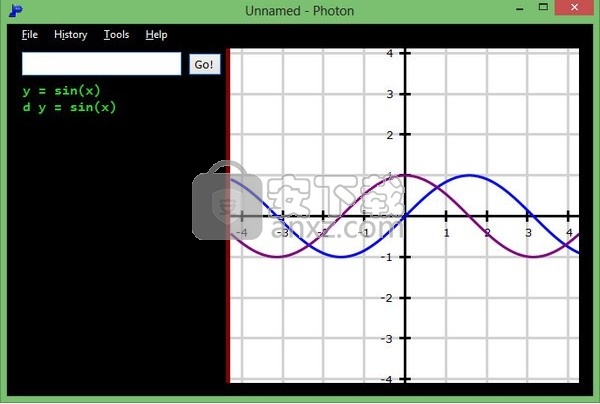
　　Photon提供图像化分析功能，可以在软件输入函数建立图表分析数据，您可以在软件输入任意函数，例如在软件输入二次函数，输入抛物线函数，软件立即生成相关的函数图，对于喜欢通过函数分析问题的朋友很适合，也可以通过这款软件快速生成教学使用的函数图，生成以后保存为图像就可以插入到试题使用，提供高亮颜色设置，不同的数据显示不同的颜色，一眼看懂数据走势，您可以在软件分析变量函数，可以在坐标轴查看函数图像，直接录入方程表达式就可以转换为适合自己使用的函数图，如果你需要这款软件就下载吧！

软件功能

　　常规、参数和极坐标图绘制

　　三维图形化

　　顺序绘图

　　绘制斜率字段并查看绘制的解法

　　绘制矢量场和计算线积分。

　　评估有限和(西格玛符号)

　　坐标空间U-V(或U-V-W)的变换。

　　轻松缩放（鼠标滚轮）和平移（鼠标拖动）。

　　用标准运算顺序计算表达式

　　程度/半径模式

　　追踪/动画

　　对数/半对数图形

　　找出根，最小/最大，和拐点。

　　评估导数和积分

　　数据绘制和拟合

　　矩阵数学（11种操作--加法、乘法、反法、行列式、Rref等。

　　分数模式(显示分数、简化平方根和圆周率系数)

　　保存文件为图像

　　在需要的地方自动插入*和^(2x变成2*x)

　　变量和函数的创建

　　可使用VBScript编程

　　使用mimeTeX的动态方程渲染。

　　快速的单位转换和摩尔质量计算

　　列表的简单统计信息，例如：五位数摘要

　　方程参考库，方便快速查询

软件特色

　　1、Photon提供很多计算功能，可以在软件计算化学

　　2、可以在软件计算数学，输入表达式就可以显示图像

　　3、软件已经收集了近百种公式，很多化学常用的公式都可以在软件输入

　　4、自动按照用户设定的变量数值转换为图像

　　5、提供坐标切换功能，可以在软件右上角选择新的坐标

　　6、可以在软件分析多种复杂的函数公式

　　7、提供保存功能，显示的函数图可以保存为JPG

使用说明

　　1、打开软件提示输入功能，在软件上输入公式，可以从菜单界面选择一种公式

　　2、软件可以分析的内容很多，您可以分析函数图像，可以在软件创建分析图，软件顶部显示很多坐标图，鼠标点击就可以切换使用

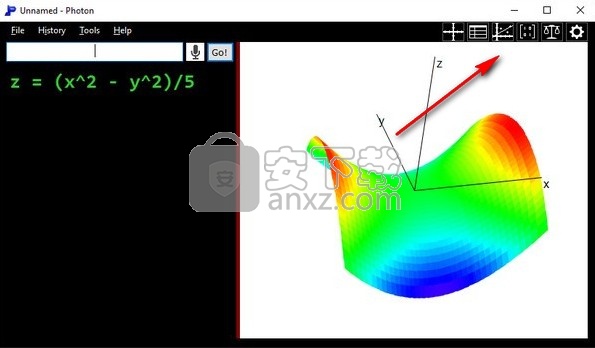
　　3、在这里输入公式，可以参考公式文档学习输入函数表达式的方法

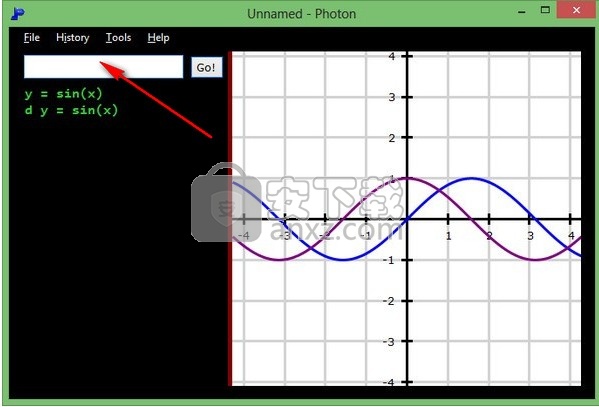
表达式

　　公共功能LCM（n1，n2）

　　a = int（n1）

　　b =整数（n2）

　　lcm =（a / gcf（a，b））* b

　　结束功能

　　公共功能GCF（n1，n2）

　　p = Int（Abs（n1））

　　q =整数（Abs（n2））

　　温度= 0

　　而（q <> 0）

　　温度= p Mod q

　　p = q

　　q =温度

　　温德

　　gcf = p

　　结束功能

　　公共职能nCk（N，K）

　　结果= 1

　　对于i = 1到K

　　结果=结果*（N-（K-i））

　　结果=结果/ i

　　下一个

　　nCk =结果

　　结束功能

　　公共职能nPk（N，K）

　　结果= 1

　　对于i =（N-K）+1至N

　　结果=结果* i

　　下一个

　　nPk =结果

　　结束功能

　　公共功能iAdd（re1，im1，re2，im2）

　　iAdd =（re1 + re2）＆“ +”＆（im1 + im2）＆“ i”

　　结束功能

　　公共功能iSub（re1，im1，re2，im2）

　　iSub =（re1-re2）＆“ +”＆（im1-im2）＆“ i”

　　结束功能

　　公共功能iMult（re1，im1，re2，im2）

　　iMult =（re1 * re2-im1 * im2）＆“ +”＆（re1 * im2 + re2 * im1）＆“ i”

　　公共功能箱（long_value）

　　hex_string =十六进制（long_value）

　　hex_string =右（String（8，“ 0”）＆hex_string，8）

　　对于digit_num = 8至1步骤-1

　　digit_value = CLng（“＆H”＆Mid（hex_string，digit_num，1））

　　因子= 1

　　nibble_string =“”

　　对于位= 3至0步骤-1

　　如果digit_value和Factor然后

　　nibble_string =“ 1”＆nibble_string

　　其他

　　nibble_string =“ 0”＆nibble_string

　　万一

　　因子=因子* 2

　　下一个

　　result_string =半字节字符串和result_string

　　下一个

　　bin = CLng（result_string）

　　结束功能

　　公共函数叉（x1，y1，z1，x2，y2，z2）

　　s1 = y1 * z2-y2 * z1

　　s2 =-（x1 * z2-x2 * z1）

　　s3 = x1 * y2-x2 * y1

　　结果= s1＆“ i +”＆s2＆“ j +”＆s3＆“ k”

　　结果=替换（结果，“ +-”，“-”）

　　结果=替换（结果，“ +”，“ +”）

　　交叉=结果

　　结束功能

　　公共功能点（x1，y1，z1，x2，y2，z2）

　　点= x1 * x2 + y1 * y2 + z1 * z2

　　结束功能

　　公共函数toComp（mag，ang）

　　s1 = mag * f2（ang）

　　s2 = mag * f1（ang）

　　结果= s1＆“ i +”＆s2＆“ j”

　　结果=替换（结果，“ +-”，“-”）

　　结果=替换（结果，“ +”，“ +”）

　　toComp =结果

　　结束功能

　　公用函数toCompZ（mag，ang1，ang2）

　　s1 = mag * f2（ang1）* f1（ang2）

　　s2 = mag * f1（ang1）* f1（ang2）

　　s3 = mag * f2（ang2）

　　结果= s1＆“ i +”＆s2＆“ j +”＆s3＆“ k”

　　结果=替换（结果，“ +-”，“-”）

　　结果=替换（结果，“ +”，“ +”）

　　toCompZ =结果

　　结束功能

　　公共函数toMagAng（x，y）

　　如果（deg = 1）那么

　　angSign =“ rad”

　　其他

　　angSign =“ deg”

　　万一

　　mag = sqr（x * x + y * y）

　　如果（x> 0）则

　　ang = af3（y / x）

　　ElseIf（x <0）然后

　　ang = af3（y / x）+ PI /度

　　其他

　　如果（y> 0）然后

　　ang =（PI / 2）/度

　　ElseIf（y <0）然后

　　ang =（-PI / 2）/度

　　其他

　　ang = 0

　　万一

　　万一

　　toMagAng = mag＆“ @”＆ang＆“”和angSign

　　结束功能

公式列表

　　活化能ln（k）= \（-\ frac {E_a} {R} \）\（\ frac {1} {T} \）+ ln（A）

　　阿雷尼厄斯方程k = Ae ^ {-E_a / RT}

　　阿伏加德罗定律V = kn

　　沸点高程\ Del {T_b} = K_bm

　　博伊耳定律P_1V_1 = P_2V_2

　　布拉格方程2d {sin} \ th = \ nu \ lambda

　　摄氏度到华氏度^ oF = {^ o} C \ times \ frac {9} {5} +32

　　摄氏度到开尔文K = {^ o} C + 273.15

　　查理定律\ frac {V_1} {T_1} = \ frac {V_2} {T_2}

　　合并气体定律\ frac {P_1V_1} {T_1} = \ frac {P_2V_2} {T_2}

　　共轭酸碱对K_aK_b = K_w

　　道尔顿分压定律P_i = X_iP_T

　　DeBroglie关系\ lambda = \ frac {h} {mv}

　　pH的定义pH = -log [H ^ +]

　　pOH的定义pOH = -log [OH ^-]

　　密度d = \ frac {m} {V}

　　气体的密度或摩尔质量d = \ frac {PM} {RT}

　　溶液的稀释度M_iV_i = M_fV_f

　　偶极矩\ mu = Q \ times {r}

　　电动势F_ {el。} = k \ frac {q_1q_2} {r ^ 2}

　　光子能量E = h \ nu

　　氢中电子的能量E_n = -R_H \（\ frac {1} {n ^ 2} \）

　　发射光子的能量\ Del {E} = h \ nu = R_H \（\ frac {1} {{n_i} ^ 2}-\ frac {1} {{n_f} ^ 2} \）

　　焓变\ Del {H} = \ Del {E} + P \ Del {V} \\\ Del {E} = \ Del {H} -RT \ Del {n}

　　焓定义H = E + PV

　　熵变\ Del {S} = \ frac {q} {T}

　　平衡常数\ Del {G ^ o} =-RTln（K）

　　华氏度到摄氏^ oC = \ frac {5} {9} \ times \（^ oF-32 \）

　　热力学第一定律\ Del {E} = q + w

　　一阶反应\ frac {[A] _o} {[A]} = kt \\ ln [A] =-kt + ln [A] _o

　　自由能变化\ Del {G} = \ Del {H} -T \ Del {S}

　　冻结点降低\ Del {T_f} = K_fm

　　一阶反应的半衰期t_ {1/2} = \ frac {ln2} {k} = \ frac {0.693} {k}

　　热容定义C = ms

　　热变化q = ms \ Del {t} \\ q = C \ Del {t}

　　亨德森·哈塞尔巴赫方程式pH = pK_a + log \ frac {[conj.base]} {[acid]}

　　亨利定律c = kP

　　理想气体定律PV = nRT

　　水的离子产物常数K_W = [H ^ +] [OH

　　元素的组成百分比{％} comp = {\ frac {n \ times {M_e}} {M_c}}} \ times100％

　　电离百分比％ionization = \ frac {[ion.acid]} {[initial.acid]} \ times100％

　　收益率{％} yield = \ frac {actual} {theory} \ times100％

　　势能V = k \ frac {q_1q_2} {r}

　　拉乌尔定律P_1 = X_1P ^ o_1

　　两种不同温度下的速率常数ln \ frac {k_1} {k_2} = \ frac {E_a} {R} \（\\ frac {T_1-T_2} {T_1T_2} \）

　　速率定律表达率= k [A] ^ x [B] ^ y

　　反应商\ Del {G} = \ Del {G ^ o} + RTln（Q）

　　Kp和Kc之间的关系K_p = K_c（0.0821 \ times {T}）^ {\ Del {n}}

　　气体分子的RMS速度v_ {rms} = \ sqrt {\ frac {3RT} {M}}

　　热力学第二定律自发：\\\ Del {S_ {univ}} = \ Del {S_ {sys}} + \ Del {S_ {surr}}> 0 \\ Equilibrium：\\\ Del {S_ {univ}} = \ Del {S_ {sys}} + \ Del {S_ {surr}} = 0

　　二阶反应\ frac {1} {[A]} = \ frac {1} {[A] _o} + kt

　　标准焓\ Del {H ^ o} _ {rxn} = \ sum {n \ Del {H ^ o} _f（产品）-\ sum {m \ Del} H ^ o（反应物）

　　标准熵变\ Del {S ^ o} _ {rxn} = \ sum {nS ^ o}（产品）-\ sum {mS ^ o}（反应物）

　　标准自由能变化\ Del {G ^ o} _ {rxn} = \ sum {n \ Del} G ^ o_f（产品）-\ sum {m \ Del} G ^ o_f（反应物）

　　不确定性原则\ Del {x} \ Del {p} \ ge \ frac {h} {4 \ pi}

　　范霍夫系数i = \ frac {#part。} {＃form.unit}

　　范德华方程（P + \ frac {an ^ 2} {V ^ 2}）（V-nb）= nRT

　　蒸气压lnP =-\ frac {\ Del {H_ {vap}}} {RT} + C \\ ln \ frac {P_1} {P_2} = \ frac {\ Del {H_ {vap}}} {R} \ （\ frac {T_1-T_2} {T_1T_2} \）

　　波长和频率v = \ lambda {\ nu}

　　气体膨胀或压缩完成的工作w = -P \ Del {V}