CGAL(计算几何算法库)

　　CGAL可以帮助用户快速搭建计算系统，当你需要分析数据和计算的时候就可以从这款软件添加相关的计算模块，CGAL中的算法和数据结构由其使用的对象类型和操作进行参数化，它们与满足特定语法和语义要求的任何具体模板参数一起使用，CGAL提供了不同的内核，它们可以因对象的内部表示而不同（例如笛卡尔或同质），也可以提供不同的功能（例如循环内核），创建新软件包时，作者必须明确指定所使用内核的要求，例如他们可以指定关于算术的需求，作者可以在预定义的内核列表（例如Exact_predicates_inexact_constructions_kernel）中指定目标内核，如果你需要CGAL就下载吧！

软件功能

　　计算几何算法库（CGAL）是一个C ++库，旨在提供对计算几何中高效而可靠的算法的轻松访问。

　　算术和代数

　　组合算法

　　几何核

　　凸壳算法

　　多边形

　　细胞复合体和多面体

　　安排

　　三角测量

　　伏罗尼图

　　网格生成

　　形状重建

　　几何处理

　　空间搜索

　　几何优化

　　插值

　　支持图书馆

　　视觉化

软件特色

　　CGAL程序包通常提供图形演示，以演示程序包中的功能。很多时候，该演示只是程序的高级版本，在开发的早期就用作（图形）调试工具。在许多情况下，几何算法的输出比数字形式更容易以图形形式解释。因此，您应该使用CGAL强大的图形输出功能进行开发

　　可用于调试程序包内部工作的程序（即用户可能无法访问的内容）

　　有趣且内容丰富的演示，突出显示了功能，同时还介绍了程序包中是否存在错误。可以在demo每个内部发行版和CGAL安装目录中找到其他演示/调试程序。

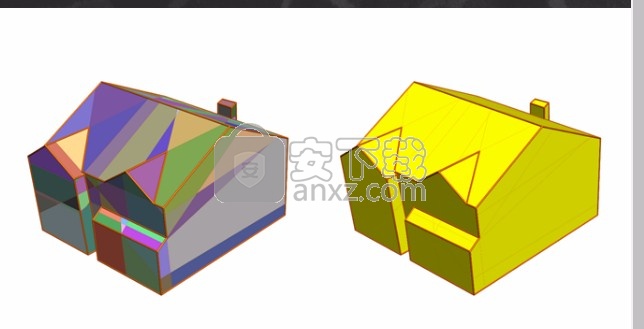
　　稳健性问题

　　几何算法的设计和正确性证明通常采用精确的算法。由于不精确的计算会导致算法的控制流中错误的决策，甚至导致相互矛盾的决策，因此许多实现都会崩溃，或者充其量只能为某些输入计算垃圾。对于某些应用程序，不良输入与所有可能的输入相比所占的比例很小，但是对于其他应用程序，此比例却很大。

　　CGAL具有分层设计。某些组件的正确性取决于所使用组件的正确性。组件的正确性是指根据其（数学）规范进行的行为。简而言之，鲁棒性问题的根源在于默认的硬件支持的算法不能真正满足算法要求，因为它没有对实数执行算法。

　　但是，由算法（更确切地说，由数字类型）参数化的内核原语的一般实现假定插入的算法的确表现为真实的算法。通用代码不会也不应（否则会减慢“精确”数字类型）处理任何潜在的不准确性。有许多（完全由第三方提供）“精确”数字类型可用于CGAL，其中“精确”表示所有决策（比较操作）都是正确的，并且数字的表示形式允许精确到任意精度， 如果需要的话。根据所需的计算，合适的确切数字类型可以是Quotient或gmpq如果涉及理性计算。如果需要多项式的根，则解决方案是使用leda_realLEDACORE::Expr提供的或CORE提供的。

　　谓词和构造的作用

　　CGAL支持将基本算术运算（即几何计算中的最低级别）封装为较高级别（即几何图元的级别，即谓词和构造）中的单元。在这里，谓词在广义上使用，即，不仅原语返回布尔值，而且原语返回某种枚举类型的值，例如CGAL::Sign。因此，谓词计算的值不包含任何数值数据。基本构造构造可能涉及新计算的数值数据的新原始几何对象，即，这不是构造输入的一部分。这种基本构造的一个示例是计算两个给定点之间的直线段的中点。选择是一种特殊的构造。对于选择，构造对象中的所有数据已经是输入的一部分。一个示例是为两个给定的点计算字典上较小的点。

　　CGAL提供了几何图元的通用实现。这些假设为“精确计算”。根据实际的数字输入数据，此方法可能有效或无效。CGAL还提供了[1]原语的专业化，这些原语（仍然是相当通用的）可以保证精确的谓词结果，并且比诸如任意精度整数或有理数之类的精确数字类型具有更高的效率。效率依赖于快速浮点算法的使用，以滤除可靠的浮点计算。间隔算术主要用于此类滤波步骤。

使用说明

　　CGAL的配置变量摘要

　　大多数配置变量不是环境变量，而是CMake变量。通过-D选项将它们在命令行中提供给CMake ，或从的交互式界面传递cmake-gui。除非另有说明，否则以下总结的所有变量均为CMake变量。

　　1.1 元件选择

　　以下布尔变量指示要配置和构建的CGAL组件。它们的值可以为ON或OFF。

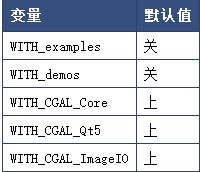
　　1.2 编译器和链接器标志

　　以下变量指定编译器和链接器标志。每个变量都包含一个用于编译器和链接器的命令行开关的空格分隔列表，它们的默认值由CMake根据目标平台自动定义。

　　请记住，这些变量指定了一个标志列表，而不仅仅是一个标志。如果您为变量提供自己的定义，则将完全覆盖CMake为该特定变量选择的标志列表。

　　与调试和发行版本相对应的变量始终与特定版本类型的变量结合使用。

　　1.3 附加的编译器和链接器标志

　　以下变量可用于添加标志，而不会覆盖cmake定义的标志。

　　1.4 杂项变量

　　请注意，默认的构建类型为Debug，仅应用于调试，并且将限制服务器的性能。

　　1.5 仅在构建程序时使用的变量（例如演示或示例）

　　1.6 提供有关第三方库信息的变量

　　以下变量提供有关CGAL使用的第三方库的可用性和位置的信息。CMake自动搜索依赖关系，因此，如果CMake无法找到某些内容，则需要指定这些变量。这由以结尾的值表示NOTFOUND。

　　由于第三方库是系统范围的，因此下面列出的许多CMake变量也可以替代地用作名称相似的环境变量。请记住，您必须提供一个或另一个，但不能两者都提供。

　　1.7 提升图书馆

　　在大多数情况下，如果没有自动找到Boost，则设置BOOST_ROOT变量就足够了。如果不是，则可以分别指定头目录和库目录。如果在库目录中找不到特定的编译库或它的名称是非标准的，则还可以提供其完整路径名。

　　默认情况下，当需要Boost二进制库时，将使用共享版本（如果存在）。您可以设置变量CGAL_Boost_USE_STATIC_LIBS来ON，如果你想用明确的静态版本链接。

　　在Windows上，如果与Boost共享库链接，则必须确保.dll在运行时由动态链接器找到文件。例如，您可以将Boost 的路径添加.dll到PATH环境变量。

　　1.8 GMP和MPFR库

　　在Windows下，使用自动链接，因此仅需要包含库的目录，您可以指定GMP|MPFR_LIBRARY_DIR而不是GMP|MPFR_LIBRARIES。另一方面，在Linux下，需要实际的库文件名。因此，您可以指定GMP|MPFR_LIBRARIES。在任何情况下，您都无需同时指定两者。

　　CGAL同时使用Gmp和Mpfr，因此都需要支持。如果其中一个都不可用，将禁用Gmp和Mpfr。

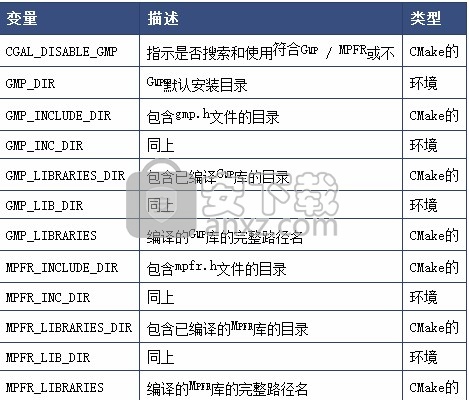
　　在Linux下，还将搜索Gmpxx，您可以指定以下变量：

　　1.9 Qt5库

　　您必须将cmake或environment变量设置Qt5_DIR为指向包含Qt 5安装Qt5Config.cmake创建的文件的目录的路径。如果您使用的是开源版本，则应为。/qt-everywhere-opensource-src-/qtbase/lib/cmake/Qt5

　　1.10 LEDA图书馆

　　当没有自动找到LEDA库时，它们以基本名称“ leda”和“ ledaD”（分别针对发行版和调试版）安装在系统上，仅通过LEDA_LIBRARY_DIRS变量指示库目录就足够了。如果由于名称不同（例如，名称不同）不起作用，则可以通过LEDA_LIBRARY_RELEASE和提供每个变体的完整路径名LEDA_LIBRARY_DEBUG。

　　如果LEDA不需要指定变量的定义和标志，则可以不定义它们。

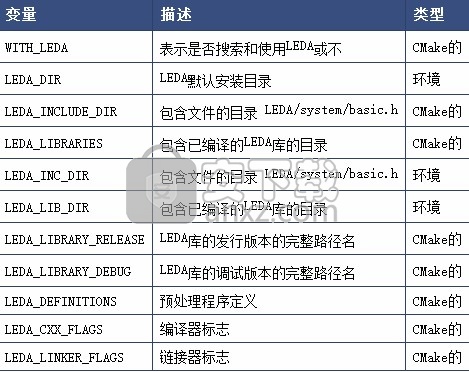
　　1.11 MPFI库

　　CGAL提供基于此库的数字类型，但是CGAL库本身不依赖于Mpfi。这意味着在编译使用上述数字类型的应用程序时必须配置此库。

　　当Mpfi文件不在标准路径上时，必须使用环境变量指定头文件和库文件的位置。

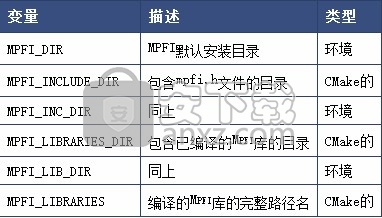
　　1.12 RS和RS3库

　　如前所述，只有CGAL单变量代数内核取决于库Rs。由于代数内核未作为CGAL库的一部分进行编译，因此在安装时不会检测或配置此库。

　　CMake将尝试在标准头文件和库目录中找到Rs。如果未自动检测到，则必须使用环境变量指定头文件和库文件的位置。

　　Rs需要Gmp 4.2或更高版本以及Mpfi 1.3.4或更高版本。与后一个库相关的变量也可能需要定义。

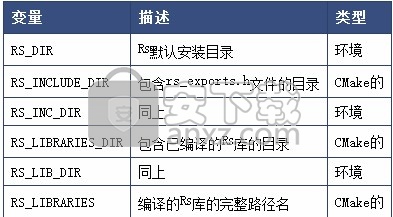
　　Rs3存在类似的变量。

　　1.13 NTL库

　　当Ntl可用时，CGAL代数内核中的某些多项式计算会加快。由于代数内核未作为CGAL库的一部分进行编译，因此在安装时不会检测或配置此库。

　　CMake将尝试在标准头文件和库目录中找到Ntl。如果未自动检测到，则必须使用环境变量指定头文件和库文件的位置。

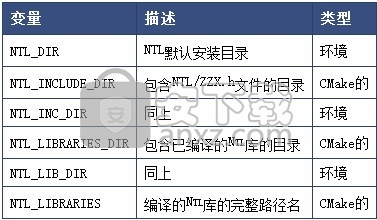
　　如何在CMake中使用CGAL

　　本页将说明如何手动创建CMakeLists.txt文件以将自定义程序与CGAL链接。

　　可以使用脚本创建基础cgal_create_CMakeLists

　　与CGAL链接

　　要与CGAL库链接，请使用以下命令：

　　其他CGAL库的链接类似。例如，使用CGAL_Core：

　　注意

　　该CGAL目标定义以下编译器标志：

　　-frounding-math 与海湾合作委员会

　　/fp:strict /fp:except- 与MSVC

　　使用Qt5的最小示例

　　本节介绍了将CGAL和Qt5用于某些GUI功能的程序的最小示例。

　　CMakeLists.txt

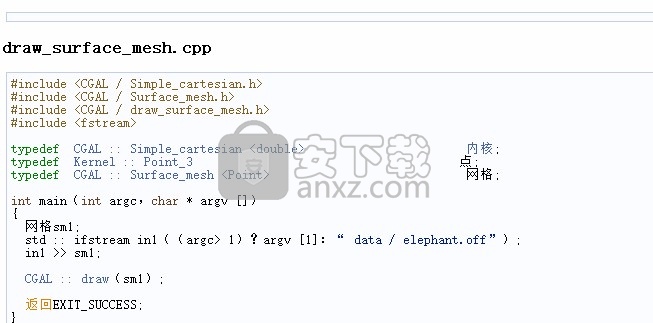
主要设计目标

　　正确性

　　如果库组件按照其规范运行，则它是正确的。因此，从根本上说，正确性是验证文件与实现是否一致的问题。在模块化程序中，模块的正确性取决于其自身的正确性以及所依赖的所有模块的正确性。显然，为了获得正确的结果，必须使用正确的算法和数据结构。

　　从可靠性的意义上讲，准确度不应与正确性相混淆。计算近似解而不是精确解的算法没有什么错，只要清楚记录了它们的行为并且确实按照指定的方式工作即可。此外，尽管在CGAL中我们希望提供处理退化的算法，但是仅处理非退化情况的算法就其规范而言可能是正确的。

　　坚固性

　　与几何算法的实现特别相关的设计目标是鲁棒性。几何算法的许多实现由于精度问题而缺乏鲁棒性。有关CGAL中的健壮性问题的讨论，请参见“健壮性问题”一章。

　　灵活性

　　潜在应用领域的不同需求要求库具有灵活性。可以确定灵活性的四个子问题。

　　模块化。

　　将CGAL清晰地构造为具有尽可能少的依赖性的模块有助于用户学习和使用CGAL，因为可以更轻松地掌握整体结构，并且可以将重点缩小到实际感兴趣的那些模块。

　　适应性强。

　　CGAL可能会在已经建立好的具有几何类和算法的环境中使用，在这种情况下，模块很可能需要使用之前进行调整。

　　可扩展性。

　　CGAL不能满足所有愿望。用户可能要扩展库。将新的类和算法集成到CGAL中应该是可能的，并且实际上是合乎需要的。

　　开放性

　　CGAL应该开放与其他库共存，或者更好地与其他库和程序一起工作。在C ++标准[4]

　　使用C ++标准库定义了所有C ++平台的通用基础。因此，遵循此标准可以轻松自然地获得开放性。标准之外还有重要的库，CGAL也应易于适应它们。

　　使用方便

　　许多不同的品质可以有助于简化库的使用。哪个质量最重要取决于用户的体验。上述的正确性和鲁棒性问题就是这些质量。一般而言，重要的是库变得有用之前需要的时间长度。另一个问题是必须学习和记住的新概念和一般规则的例外。

　　易于使用往往会与灵活性产生冲突，但是在许多情况下都可以找到解决方案。CGAL的灵活性不应分散初学者使用CGAL的注意力。

　　均匀性

　　CGAL中设计的统一外观将有助于学习和记忆。一经学习的概念应适用于希望应用的所有地方。一旦为特定类学习到的函数名称，不应为另一个类使用不同的名称。

　　CGAL在许多地方都基于从STL（标准模板库）或C ++标准库的其他部分借来的概念。一个示例是在CGAL中使用流和流运算符。另一个示例是使用STL中的容器类和算法。因此，这些概念应统一使用。

　　在过去的几年中，CGAL转向使用boost库中的概念和思想，并提供指向boost库的接口。这些包括增强图形库和增强属性映射库。

　　完整和最小的接口。

　　具有相同含义的目标是具有完整和最少接口的设计，例如，参见参考资料中的第18项。[9]。对象或模块的功能应完整，但不应提供其他修饰功能。即使某个功能看起来像有助于某个班级的易用性，但从更全局的角度来看，它可能会妨碍对班级间异同的理解，并使学习和记忆更加困难。

　　丰富而完整的功能。

　　我们的目标是收集有用且丰富的几何类，数据结构和算法。CGAL被认为是计算几何中算法研究的基础，因此需要一定的广度和深度。该领域的标准技术应该出现在CGAL中。

　　完整性也与鲁棒性有关。

　　我们的目标是提供通用解决方案，例如，不受一般职位假设的限制。CGAL中的算法应能够处理特殊情况和简并性。

　　在事实证明退化的处理效率低下的情况下，除了处理所有退化的通用算法外，还应在库中提供更有效但通用性较低的特殊变体。当然，需要清楚地记录哪些退化被处理，哪些不被处理。

　　效率

　　对于大多数几何算法，时间和空间复杂度的理论结果是已知的。而且，与最坏情况相反，对实际输入的效率的理论兴趣也在增长[13]。出于实际目的，有必要洞悉隐藏在标记中的常量因子，尤其是在存在几种竞争算法的情况下。O因此，如果没有一个最佳解决方案，则应提供不同的实现方式，例如，当在时间和空间之间进行权衡时，或者在没有或几乎没有简并性的情况下实现更有效的实现方式。